La Toolbox GRESIPOL propose une formation de 39h sur des problématiques
environnementales et industrielles essentielles :
1) la gestion de ressources en eaux souterraines et la vulnérabilité des hydrosystèmes
vis-à-vis des activités anthropiques ;
2) la gestion des sites et sols pollués.
Les outils de simulation des écoulements dans les aquifères sont des outils essentiels pour la compréhension des mouvements des eaux souterraines et pour leur gestion.
Le service géologique fédéral des USA (USGS, US geological survey) met à disposition toute une série de codes dédiés à la gestion des ressources en eau. Ces codes sont libres et gratuits et les sources (en FORTRAN) sont disponibles.
MODFLOW est le code USGS dédié à la simulation des écoulements en milieu poreux. Son développement remonte aux années 1980, de nombreux codes d’écoulement et transport en milieu poreux sont apparus depuis, mais MODFLOW, qui est l’objet de refontes régulières (tous les 5 à 10 ans, la dernière refonte, MF6, datant de 2017 ), reste le code de référence dans le domaine de la simulation des aquifères.
Le code MODFLOW lui-même est comme on l’a dit open source, mais pratiquement impossible à utiliser sans outils dédiés de pre-processing (concevoir les fichiers d'entrée décrivant le problème à traiter) et de post-processing (édition et visualisation des résultats). Ces outils sont en général commerciaux, et des licences ont été acquises par l'école pour Visual Modflow et Groundwater Vista, mais une alternative gratuite, flopy, est apparue ces dernières années. Développée en partie par des chercheurs de l’USGS, elle permet l'utilisation de MODFLOW sous ses différentes versions et de la plupart des codes USGS dédiés à l’écoulement et au transport dans les aquifères (MODPATH, SEAWAT, MT3DMS).
À la différence de Visual Modflow, flopy n'est pas un logiciel dédié mais une bibliothèque de classes Python qui permettent de gérer les différents modules d'un projet MODFLOW, de lancer le calcul et de lire et visualiser les résultats.
On se propose d'abord d’installer flopy et les programmes USGS nécessaires, dans le but d’utiliser non seulement MODFLOW, mais aussi le code MT3DMS qui permettra de mettre en œuvre des simulations de transport de contaminants en milieu poreux.
flopy étant une librairie pour python 3, il vous faudra disposer de python 3 sur votre machine pour l’utiliser.
On propose de commencer par installer flopy et les programmes USGS nécessaires, dans le but d’utiliser non seulement MODFLOW, mais aussi le code MT3DMS qui permettra de mettre en œuvre des simulations de transport de contaminants en milieu poreux.
flopy étant une librairie pour python 3, il vous faudra disposer de python 3 sur votre machine pour l’utiliser.
>> installer python, flopy, modflow
MODFLOW est un programme développé par l'USGS (U S Geological Survey) pour modéliser les écoulements dans les aquifères. Introduit en 1983, développé en fortran et disponible en open source, il a connu de nombreuses évolutions. Il peut être considéré comme le programme de référence dans le domaine de la simulation des écoulements dans les aquifères.
"We use MODFLOW because it is freeware, open-source, well-documented, versatile, used worldwide and in the US is the standard code in regulatory and legal arenas" (in Anderson et al, APPLIED GROUNDWATER MODELING, Simulation of Flow and Advective Transport, Academic Press, 2015) .
L’objectif d’un modèle modflow est de résoudre l’équation de diffusivité,
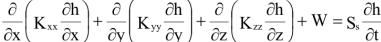
équation qui gouverne l’évolution spatio-temporelle des niveaux piézométriques d’un domaine soumis à des conditions données.
Kxx , Kyy, Kzz (L/T) =
conductivité hydraulique suivant les axes
(supposés parallèles aux principaux axes de la conductivité)
h (L) = niveau piézo (= charge, potentiometric head)
W (1/T) = flux volumétrique par unité de volume,
représente les sources et/ou puits d’eau,
W<0.0 pour les flux sortant du système,
W>0.0 pour les flux entrants
Ss (1/L) = Coefficient d’emmagasinement spécifique
t (T) = le temps.
Ss et Kii peuvent varier dans l'espace
W peut varier dans l'espace et le temps
MODFLOW résout cette équation numériquement, par discrétisation, en temps et en espace, suivant une méthode de différences finies.

Une documentation complète est disponible en ligne, par exemple pour MODFLOW-2005, dernière évolution du modèle classque:
Harbaugh, A.W., 2005, MODFLOW-2005, The U.S. Geological Surveymodular ground-water model – the Ground-Water Flow Process: U.S.Geological Survey Techniques and Methods 6-A16
>> https://pubs.usgs.gov/tm/2005/tm6A16/PDF.htm
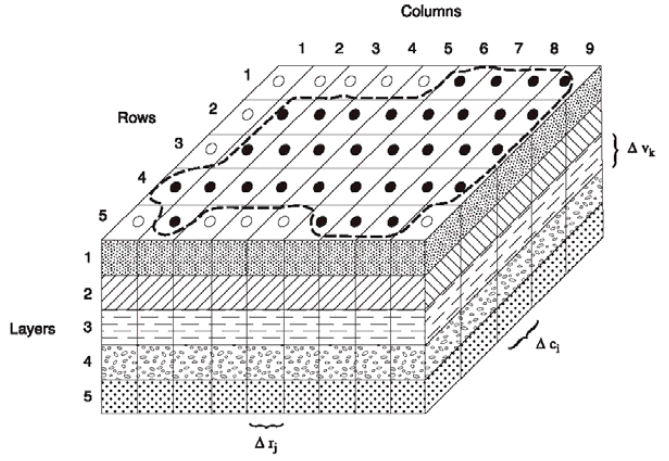
Modflow (modular flow) est organisé en modules, appelés packages. Pour construire un modèle Modflow pour traiter un cas donné, on doit assembler un certain nombre de ces packages: un module de base, un module de discrétisation, un pour les puits, s’il y en a, les rivières, etc.
A chaque module correspond un fichier, et le suffixe du nom de fichier renseigne sur la fonction du module. Typiquement, si le modèle a pour nom “tutorial_1”, les données de base seront dans un fichier tutorial_1.bas, les paramètres de maillage dans tutorial_1.dis, etc.
Les autres programmes USGS, tels que MT3DMS, suivent en général ce schéma en modules et fichiers associés.
La librairie flopy a pour objet d’écrire ces différents fichiers à partir de données inscrites en clair dans un script python. De manière générale, à chaque module MODFLOW correspond un objet flopy qui prendra en arguments les paramètres du module.
Ces modules peuvent être classés suivant les catégories décrites sur la page :
Le langage Python est de plus en plus utilisé, en particulier par les non-informaticiens. Dans de nombreux métiers d'ingénieurs, être opérationnel en python devient aussi essentiel que par exemple savoir utiliser excel. On trouvera sur internet un grand nombre de sites dédiés à l’apprentissage de python, par exemple sur le site du consortium w3c (bien pour débuter) ou sur python.org ou chez google (NB: python2), mais on peut aussi, une fois passée python installé, commencer sans formation complète et utiliser directement des programmes existants. C’est le cas ici avec les scripts de démonstration de flopy, et on pourra faire beaucoup de choses intéressantes rien qu’en modifiant quelques lignes dans un script existant.
Il est quand même nécessaire d’avoir quelques notions de base.
Un programme peut être constitué d’un seul bloc, avec une suite d’instructions telle que
initialiser calculer enregistrer / visualiser
C’est le cas d’un grand nombre des scripts de démonstration de flopy, mais, dans la plupart des cas, on doit implémenter des branchements conditionnels ou des boucles, qui introduisent alors des sous-blocs, qui peuvent eux mêmes contenir des sous-sous-blocs, etc. La structuration de ces blocs se fait en général à l’aide mots-clés ou de caractères spéciaux. Il est d’usage d’indenter le texte pour en faciliter sa lecture.
if(condition_1) then
calcul_1 ! sous-bloc 1
else
calcul_2 ! début sous-bloc 2
do i=1,6
calcul_3 ! sous-bloc 3
end do ! fin sous-bloc 2
end if
Dans la plupart des langages, cette indentation est recommandée mais n’est pas nécessaire, en Python, l’indentation est essentielle car c’est elle qui indique la hiéarchie des blocs. Indenter n’est donc pas seulement recommandé, c’est essentiel, car cela remplace, associé au caractère ‘:’, les mots-clés qui indiquent le début et la fin d’un (sous)-bloc.
L’exemple ci-dessus devient en python :
if condition_1:
calcul_1 # sous-bloc 1
else:
calcul_2 # début sous-bloc 2
for i in range(6):
calcul_3 # sous-bloc 3
Troisième chose à bien comprendre, l’indexation des tableaux (‘array’) en python. C’est essentiel pour gérer les coordonnées des objets d’un modèle modflow (coordonnées d’un puits, définition des perméabilités dans une zone donnée, etc).
Pour gérer des variables multi-dimensionnelles (c’est à dire des vecteurs et matrices, qu’on appelle ‘tableaux’ en informatique), on a d’une part les listes python, ou les objets de type array de la librairie scientifique numpy.
En python, une liste est une série de valeurs entre crochets :
well_xyz= [0, 5, 11]
définit la position d’un puits, sur la couche 0, aux coordonnées 5 et 11 en ligne et colonne respectivement.
Noter que l’indexation des tableaux débute à zéro en python (comme en langage C, java, etc), alors qu’en fortran, matlab etc l’indexation commence à 1. Aussi, comme modflow est écrit en fortran, la couche 0 en flopy correspond à la couche 1 du modèle modflow, et le point x,y= 5,11 correspond au point x,y= 6,12 ...
Pour cette raison, on trouve parfois dans les scripts flopy du code destiné à effectuer ces changements de base entre l'espace modflow et celui de flopy.
Deux scripts sont proposés pour tester l’installation de flopy et des exécutables associés, 01-tutorial01.py et 01-tutorial02.py.
Ces deux scripts sont dérivés de scripts qui sont (ou ont été) disponibles sur example/tutorials du dépôt github de flopy https://github.com/modflowpy/flopy.
Nous utiliserons aussi certains "notebooks" du répertoire Notebooks (convertis en python standard) pour illustrer les problématiques de transport d’éléments en solution, en mettant donc en œuvre MT3DMS en plus de MODFLOW.
01-tutorial01.py modélise un aquifère confiné de 1000 par 1000 mètres, sur 50 mètres d’épaisseur, horizontal, avec une conductivité hydraulique homogène, et avec des niveaux piézométriques imposés sur les bordures Est (h= 10.) et Ouest (h= 0.).
Le script est une suite de créations d’objets flopy qui correspond chacun à une package modflow, et à un fichier d’entrée pour modflow :
mf = flopy.modflow.Modflow(‘Tutorial01’, exe_name='mf2005')ici, on crée l’objet mf qui est du type Modflow défini dans le module modflow de la librairie flopy. A ce stade, l’objet mf, qui va décrire le modèle d’écoulement, ne contient qu’un nom et le nom du programme usgs qui sera appliqué au modèle ; la variable mf apparaîtra ensuite en paramètre d’entrée des instructions flopy qui vont renseigner les différentes caractéristiques de ce modèle mf.
dis = flopy.modflow.ModflowDis(mf, ...
bas = flopy.modflow.ModflowBas(mf, ...
lpf = flopy.modflow.ModflowLpf(mf, ...
oc = flopy.modflow.ModflowOc(mf, ...
pcg = flopy.modflow.ModflowPcg(mf)
mf.write_input()
success, buff = mf.run_model()
Flopy est ensuite utilisé pour exploiter les sorties de MODFLOW, en particulier pour les visualiser, par exemple par une carte des niveaux piézométriques, ou une carte des vitesses, avec en outre le maillage de discrétisation, par l’instruction
lc = mapview.plot_grid()
et le statut des cellules, les cellules à charge imposée sont en bleu :
qm = mapview.plot_ibound()

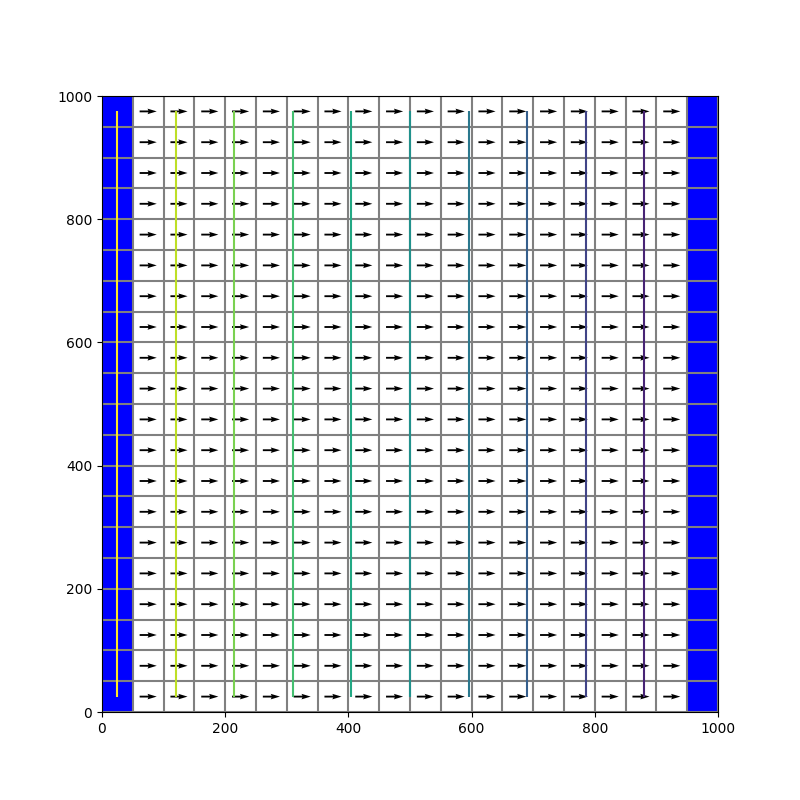
>> 01-tutorial01.py - commentaire détaillé
Pour afficher le contenu détaillé d'un objet flopy, on peut utiliser la directive print(), mais, pour écrire cela sur un fichier plutôt qu'à l'écran, on redirige momentanément la sortie standard vers un fichier, par exemple:
original_stdout = sys.stdout
fname= os.path.join('.', 'debug',filname)+'-dis.txt'
with open(fname, 'w') as f:
sys.stdout = f
print(dis)
sys.stdout = original_stdout
ce qui produit le fichier texte suivant:
Il est facile de modifier certaines caractéristiques du domaine pour voir l’impact sur les écoulements.
Par exemple, en désactivant des cellules, ou en introduisant des zones de conductivité plus faible ou plus élevée que l’ensemble.
Pour changer le statut des cellules, on intervient sur le tableau ibound, qui sera lu par flopy.modflow.ModflowBas. Noter qu'un indice néfgatif signifie qu'on compte à partir de la fin: -1 correspond au dernier élément d'un tableau.
ibound = np.ones((nlay, nrow, ncol), dtype=np.int32) ibound[:, :, 0] = -1 # icol= 0 means first column, for all x and z ibound[:, :, -1] = -1 # icol= -1 means last column, for all x and z ibound[:, 4:8,4:8]= 0 # inactive cells
Les cellules désactivées sont mises en noir par mapview.plot_ibound.
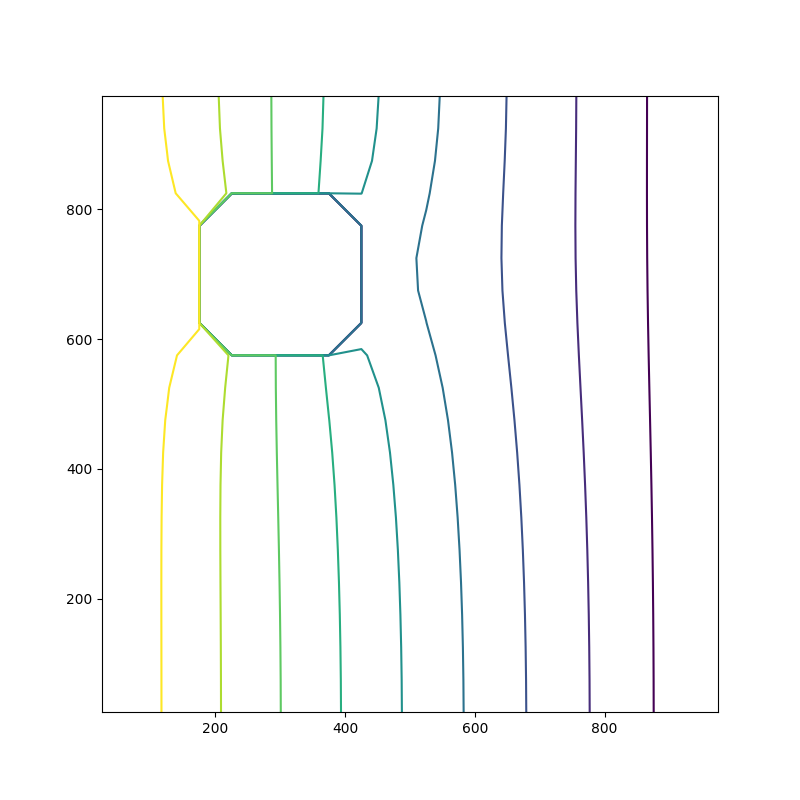
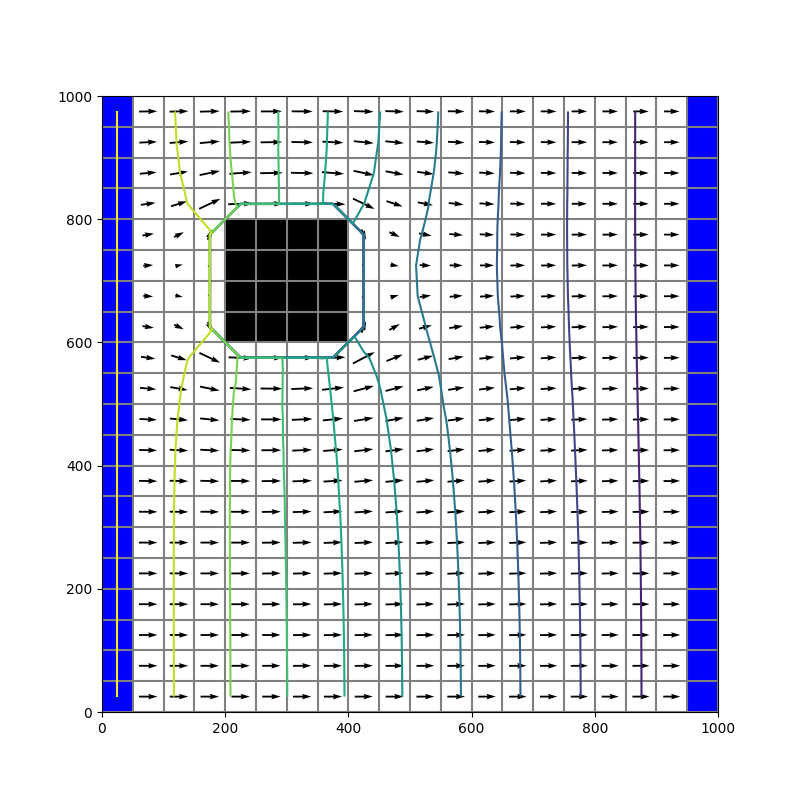
On peut aussi visualiser hl'effet d'hétérogénéités de la conductivité en faisant varier le paramètre hk. Quand hk est homogène, il est entré comme scalaire, on écrit simplement hk=10; pour pouvoir le faire varier localement, il faut donc d'abord l'initialiser comme tableau numpy 3D de réels.
hk= np.ones((nlay, nrow, ncol), dtype=np.float32) *10. hk[:, 4:8, 4:8]= 500. hk[:,12:16,12:16]= 0.1
Les flux vont s'accélérer dans la zone à hk élévé, et ralentir dans la zone à hk faible.


A la différence de tutorial01, qui calcule une solution stationnaire dans un aquifère captif, tutorial02 considère un aquifère libre et comprend une période stationnaire suivie de deux périodes transitoires, chacune de 100 jours, et divisée en 100 pas de 1 jour.
Avec ilay= 1 en entrée de flopy.modflow.ModflowLpf on a un aquifère libre.
"stress periods":
leur nombre, leurs longueurs (en jours par défaut), leurs nombres de pas, et leur nature (stationnaire ou transitoire) sont indiqués par les paramètres nper, perlen, nstp, steady, passés en entrée de ModflowDis.
nper = 3 # the number of stress periods
perlen = [1, 100, 100] # the lengths (days) of each stress period
nstp = [1, 100, 100] # the step numbers of each stress period
steady = [True, False, False]
dis = flopy.modflow.ModflowDis(
mf,
nlay, nrow, ncol,
delr=delr, delc=delc,
top=ztop, botm=botm[1:],
nper=nper, perlen=perlen, nstp=nstp,
steady=steady)
puits:
tutorial02 permet aussi de voir comment on implémente un puits de pompage (ou d’injection) et de visualiser son effet sur les écoulements.
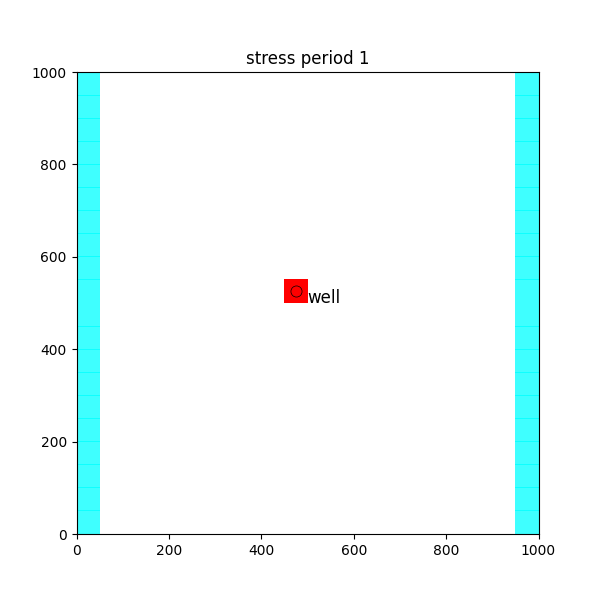
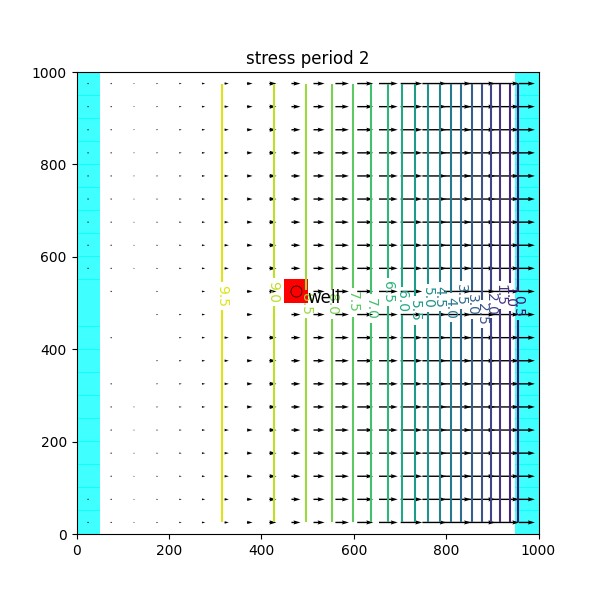
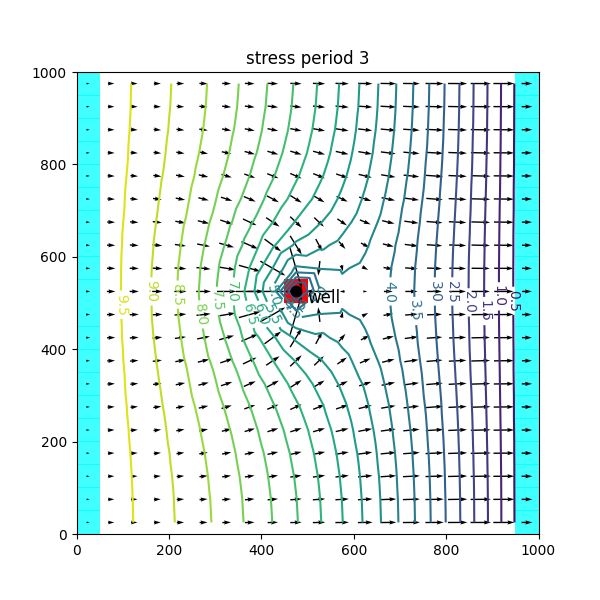
On peut jouer sur les différents paramètres, par exemple implémenter deux puits, les faire fonctionner en injection, etc. et voir la dynamique du système, l’évolution des lignes de courant et des isopièzes.
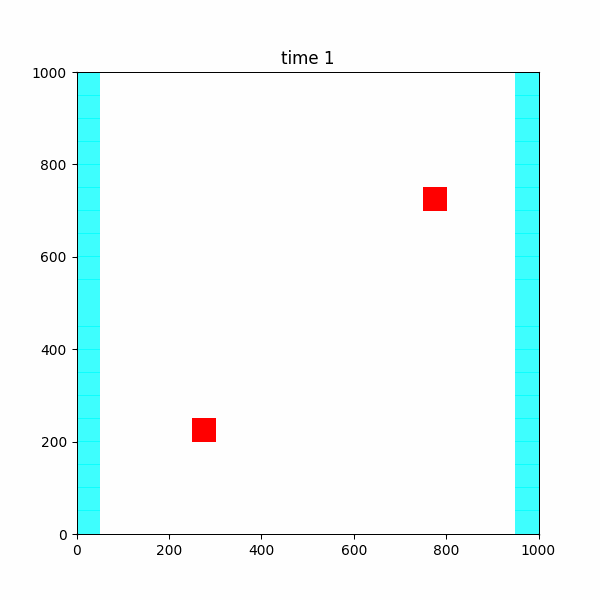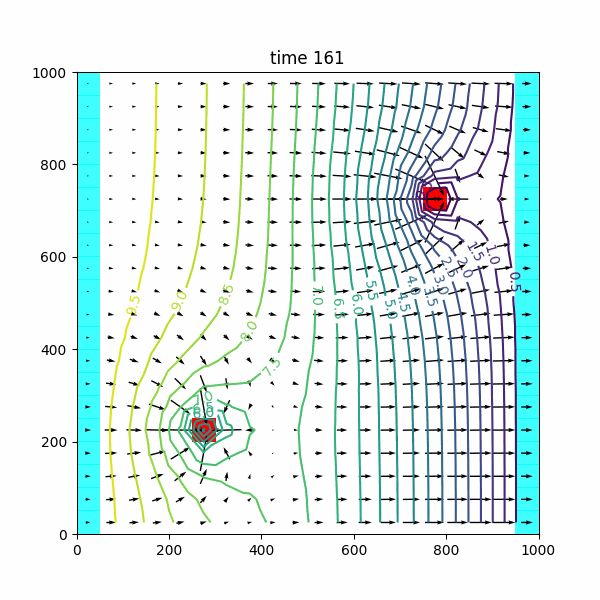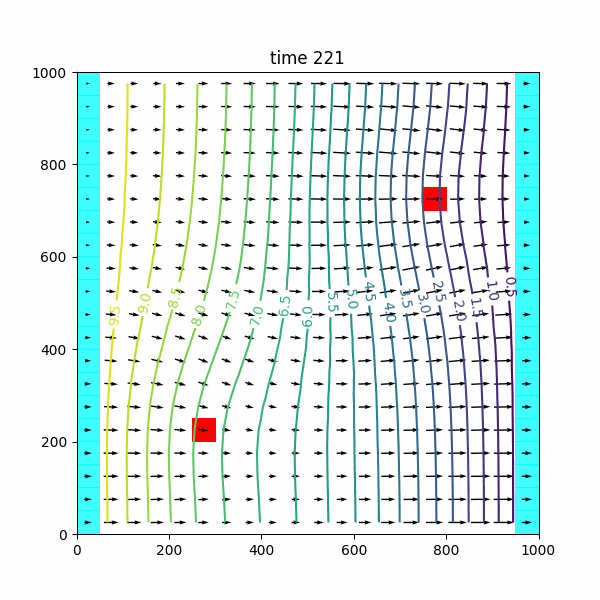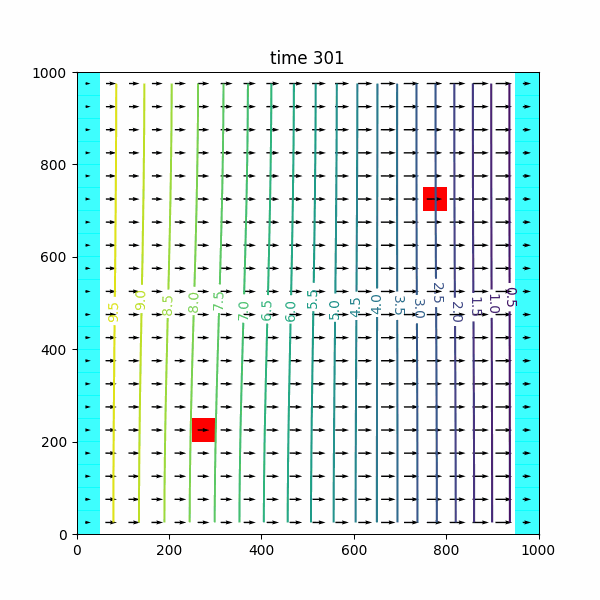
tutorial03 est dérivé de 01-tutorial02.py, avec deux puits, situés à (z,x,y)= (0,5,15) et (0,15,5), en pompage sur la deuxième période transitoire.
wel_sp1 = [[0, 5, 15, 0.], [0, 15, 5, 0.]] # t=0-1 steady
wel_sp2 = [[0, 5, 15, 0.], [0, 15, 5, 0.]] # t=1-101 transient
wel_sp3 = [[0, 5, 15, prt], [0, 15, 5, prt]] # t=101-201 transient
wel_sp4 = [[0, 5, 15, 0.], [0, 15, 5, 0.]] # t=201-301 transient
spd = {0: wel_sp1, 1: wel_sp2, 2: wel_sp3, 3: wel_sp4}
wel = flopy.modflow.ModflowWel(
mf,
stress_period_data=spd)
MT3DMS (Zheng & Wang, 1999 *) permet de simuler le transport d’espèces en solution, dans un milieu poreux, par advection, dispersion, diffusion moléculaire, avec éventuellement des termes de puits et sources.
MT3DMS (Modular Transport 3D Multi Species) calcule le transport en solution à partir d’un champ de vitesses obtenu au préalable par un run MODFLOW sur le cas étudié.
MT3DMS rassemble dans un même code plusieurs méthodes numériques pour résoudre l’équation de transport: différences finies en mode implicite (FDM,) méthode des caractéristiques (MOC) à base de particules, schéma TVD d’ordre 3 (ULTIMATE).
MT3DMS peut prendre en compte des réactions chimiques entre solution et milieu poreux, mais il se limite aux cas où il n’y a pas de rétro-action entre les réactions chimiques et propriétés hydrauliques (par exemple des réactions de dissolution / précipitation qui modifieraient localement la porosité, donc la perméabilité).
Pour un transport réactif couplé, on doit lui ajouter des modules dédiés. Le plus abouti est PHT3D, qui couple MT3DMS avec PHREEQC, mais il semble que les développements récents sur le transport réactif à USGS se font sur PHAST (PHREEQC And HST3D), qui utilise aussi PHREEQC pour la chimie, mais couplé à HST3D, un autre code USGS pour le transport, sans lien direct avec MODFLOW.
(*) Zheng, C., and Wang, P., 1999, MT3DMS: A modular three-dimensional multispecies transport model for simulation of advection, dispersion, and chemical reactions of contaminants in groundwater systems; Documentation and user’s guide. Contract Report SERDP-99-1: Vicksburg, Miss., U. S. Army Engineer Research and Development Center.
la résolution de l’équation de diffusivité par MODFLOW donne la charge hydraulique h.
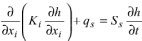
Le lien entre écoulement et transport se fait par l’équation de Darcy, qui donne les vitesses à partir des gradients de charge:
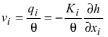
La vitesse d'advection intervient dans l'équation d'advection - diffusion - réaction qui gère le transport réactif.
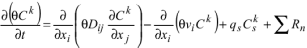
θ = porosity of the subsurface medium, dimensionless
Ck = dissolved concentration of species k, M/L3
t = time, T
xi,j = distance along the respective Cartesian coordinate axis, L
Dij = hydrodynamic dispersion coefficient tensor, L2/T
vi = seepage or linear pore water velocity, L/T
related to the specific discharge or Darcy flux
through the relationship, vi = qi / θ
qs = volumetric flow rate per unit volume of aquifer
representing fluid sources (positive) and sinks (negative), 1/T
Csk = concentration of the source or sink flux for species k, M/L3
Rn = chemical reaction term, M/L3/T
La dispersion Dij comprend deux termes:
- la dispersion mécanique, qui résulte des écarts entre la vitesse réelle à l'échelle du pore et la vitesse moyenne de l'eau souterraine,
- la diffusion moléculaire générée par les gradients de concentration.
La diffusion moléculaire est en général négligeable, comparée à la dispersion mécanique. Elle ne devient importante que lorsque la vitesse des eaux souterraines est très faible.
La somme de la dispersion mécanique + diffusion moléculaire est appelée dispersion hydrodynamique, ou simplement dispersion
Puits et sources :
Le terme puits / source de l'équation, qs Cs, représente la masse de soluté entrant dans le domaine par des sources ou quittant le domaine par des puits.
Les puits ou les sources peuvent être ponctuels ou distribués sur tout un domaine. Les puits / sources “distribués” en surface comprennent la recharge (pluie) et l'évapotranspiration. Les puits ou sources ponctuels comprennent les puits, les drains et les rivières. Les limites de domaine à charge constante ou dépendant de la charge sont également traitées dans le modèle d'écoulement comme des puits ou sources ponctuels car ils fonctionnent exactement de la même manière que les puits, les drains ou les rivières dans le modèle de transport.
Les scripts proposés sont pour la plupart dérivés des scripts de démonstration du site github de flopy.
Ils correspondent aux benchmarks décrits dans la documentation de MT3DMS. Une partie de ces benchmarks reproduisent des configurations d’écoulement et transport pour lesquelles le problème posé a une solution analytique connue, ce qui permet d'apprécier la validité des schémas numériques utilisés.
Un run MT3DMS comprend en fait deux runs successifs: d'abord un run MODFLOW qui calcule l’écoulement dans le système pour les conditions de flux des différentes périodes, ensuite un run MT3DMS calculé pour les conditions de transport sur les mêmes périodes que le modèle MODFLOW.
On commence, grâce aux objets et méthodes du module modflow de flopy, par construire mf, qui est un objet Modflow:
mf = flopy.modflow.Modflow(..., exe_name='mf2005') dis = flopy.modflow.ModflowDis(mf, ... bas = flopy.modflow.ModflowBas(mf, ... lpf = flopy.modflow.ModflowLpf(mf, ... pcg = flopy.modflow.ModflowPcg(mf) lmt = flopy.modflow.ModflowLmt(mf) mf.write_input() mf.run_model(silent=True)
Puis on construit, grâce aux objets et méthodes du module mt3d de flopy, un objet Mt3dms, avec mf comme argument:
mt = flopy.mt3d.Mt3dms(...,exe_name='mt3dms',modflowmodel=mf) btn = flopy.mt3d.Mt3dBtn(mt, ... adv = flopy.mt3d.Mt3dAdv(mt, ... dsp = flopy.mt3d.Mt3dDsp(mt, ... rct = flopy.mt3d.Mt3dRct(mt, ... ssm = flopy.mt3d.Mt3dSsm(mt) gcg = flopy.mt3d.Mt3dGcg(mt) mt.write_input() mt.run_model(silent=True)
Input Files
Name Description --- ---------------------------------- MTS MT3DMS Super File BTN Basic Transport Package File ADV Advection Package File DSP Dispersion Package File SSM Sink and Source Mixing Package File RCT Chemical Reactions Package File GCG Generalized Conjugate Gradient Solver Package File TOB Transport Observation Package File PHC PHT3D-PHREEQC Interface Package File HSS Hydrocarbon Spill Source Time-Varying Package File
Output Files
Name Description --- ---------------------------------- OUT Model Output Text File CNF Model Spatial Discretization Configuration File UCN Unformatted Concentration (Dissolved Phase) File UCN Unformatted Concentration (Sorbed/Immobile Phase) File OBS Concentration Observation File MAS Mass Budget Summary File OCN Output Concentration File MTR Unformatted Concentration (Sorbed/Immobile Phase) File PST Binary Post-Processing File MAS Mass Budget Summary File
Transport 1D dans un flux uniforme, avec advection, dispersion, et des réactions chimiques simples: détails dans Zheng & Wang, 1999, page 130
Modèle 1D, 1000 mètres en x, 1 mètre en y et en z
nlay, nrow, ncol = 1, 1, 101 delr = 10 # cell length along x delc = 1 # cell length along y delv = 1 # cell length along z perlen = 2000 # durée de simulation t = 2000 jours
Ici, pour le modèle de flux, les première et dernière colonnes sont des limites à charge constante, avec des valeurs fixées de manière à établir le gradient hydraulique uniforme requis.
ibound = np.ones((nlay, nrow, ncol), dtype=np.int) ibound[0, 0, 0] = -1 ibound[0, 0, -1] = -1 strt = np.zeros((nlay, nrow, ncol), dtype=np.float) h1 = q * Lx strt[0, 0, 0] = h1
Dans le modèle de transport, la première colonne est une frontière à concentration constante avec une concentration relative de un. La dernière colonne est placée suffisamment loin de la source pour se rapprocher d'un domaine d'écoulement unidimensionnel infini comme supposé dans la solution analytique.
v = 0.24 # vitesse d'infiltration 0.24 m/jour prsity = 0.25 # Porosité q = v * prsity c0 = 1. icbund = np.ones((nlay, nrow, ncol), dtype=np.int) # all cells are active concentration cell, except entry cell icbund[0, 0, 0] = -1 # constant-concentration cell sconc = np.zeros((nlay, nrow, ncol), dtype=np.float) # all cells have zero initial concentration, except entry cell sconc[0, 0, 0] = c0
alpha = dispersivity (metre) R = retardation factor lambda = decay rate constant (1/day) mixelm = numerical method 1a: advection seule = ADV alpha, retardation, lambda, mixelm = 0, 1, 0, 1 1b: advection et dispersion = ADV-DSP10 alpha, retardation, lambda, mixelm = 10, 1, 0, 1 1c: advection - dispersion - sorption = ADV-DSP10-RET5 alpha, retardation, lambda, mixelm = 10, 5, 0, 2 1d: advection - dispersion - sorption = ADV-DSP10-RET5-SOR alpha, retardation, lambda, mixelm = 10, 5, 0.002, 2
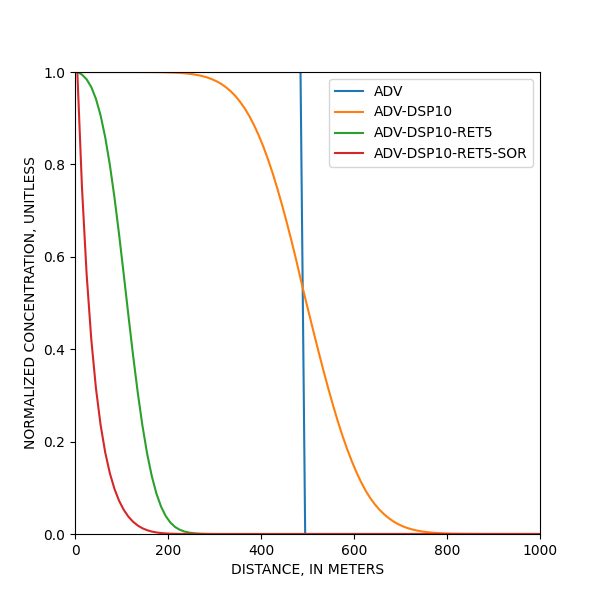
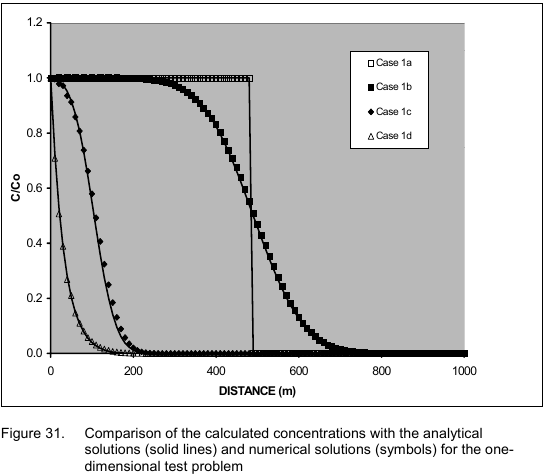
A comparer avec la figure 31 de Zheng & Wang, 1999 >>
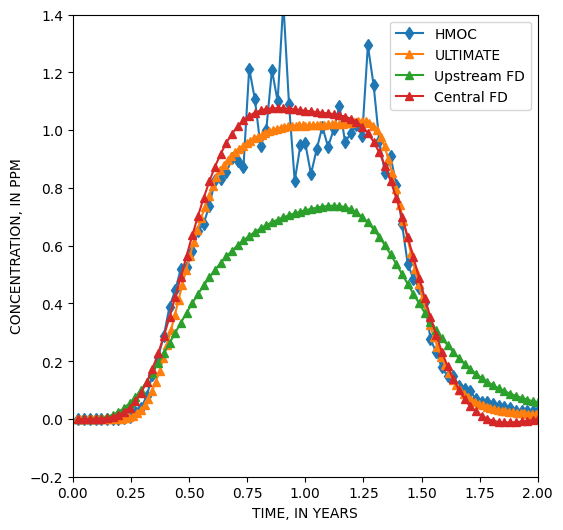
1e: advection seule, mixelm=1 = ADV-MOC alpha, retardation, lambda1, mixelm = 0, 1, 0, 1 1f: advection seule, mixelm=-1 = ADV-ULTIMATE alpha, retardation, lambda1, mixelm = 0, 1, 0, -1 1g: advection seule, mixelm=0 = ADV-Upstream-FD alpha, retardation, lambda1, mixelm = 0, 1, 0, 0 1g1: advection seule, mixelm=2 : = ADV-MMOC alpha, retardation, lambda1, mixelm = 0, 1, 0, 2 1g2: advection seule, mixelm=3 = ADV-HMOC alpha, retardation, lambda1, mixelm = 0, 1, 0, 3
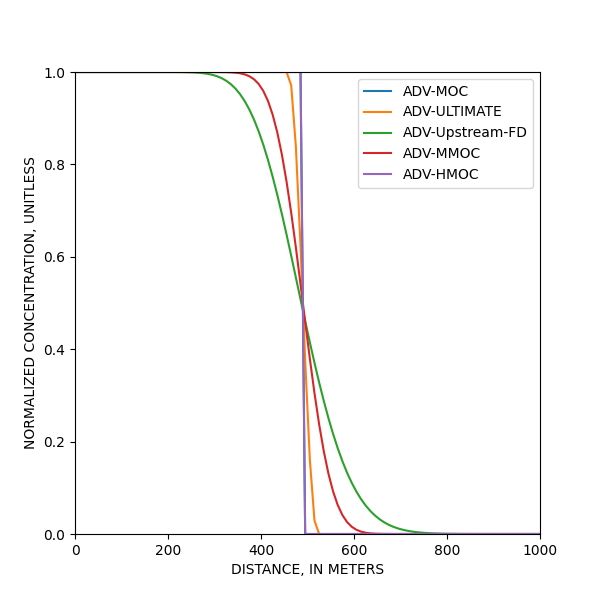
En advection pure, seul le schéma MOC (Method Of Characteristics) donne la solution. On sait en effet que l’advection pure est difficile à résoudre numériquement, et la méthode des caractéristiques a été justement développée pour les cas à advection dominante. Le schéma ULTIMATE (TVD ordre 3), qui a l’avantage d’être moins lourd numériquement, est relativement proche de la solution analytique, et il est beaucoup plus efficace que le schéma FD classique, où la “diffusion numérique” est très présente.
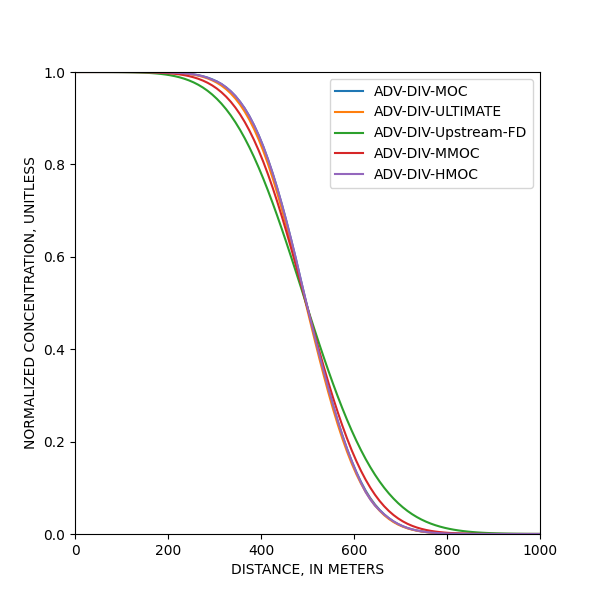
En advection-diffusion, les différents schémas fonctionnent, on peut donc, dès que Péclet est en dessous de 4, utiliser un schéma FD classique, qui est beaucoup moins intensif numériquement.
alpha, retardation, lambda = 10, 1, 0 pour tous les cas 1e10 mixelm= 1 ADV-DIV-MOC 1f10 mixelm=-1 ADV-DIV-ULTIMATE 1g101 mixelm= 0 ADV-DIV-Upstream-FD 1g102 mixelm= 2 ADV-DIV-MMOC 1g103 mixelm= 3 ADV-DIV-HMOC
Transport 1D avec réaction de sorption.
nlay = 1 nrow = 1 ncol = 101 # colonne 1D delr = .16 # grid spacing, delta x = 0.16 cm delc = 1 delv = 1 Lx = (ncol - 1) * delr v = 0.1 # vitesse infiltration (v) = 0.1 cm/s prsity = 0.37 q = v * prsity
"isotherme"
= fonction de répartition solide/gaz ou solide/liquide à une température donnée
isotherme d’adsorption de Freundlich
x = masse de l'espèce adsorbée m = masse de l'hôte adsorbant c = concentration de l'espèce en solution x/m= K c**(1/n) log(x/m)= log(K) + 1/n log(c)
isotherme d’adsorption de Langmuir
theta= fraction de sites occupés theta= K.x/(1+K.x)
paramètres des isothermes d’adsorption
Freundlich equilibrium constant (Kf) = 0.3 (µg/g)(l/mg) Freundlich sorption exponent (a) = 0.7 Langmuir equilibrium constant (Kt) = 100 l/mg Langmuir sorption capacity (S_bar) = 0.003 µg/g Concentration of source fluid C0 = 0.05 mg/l Duration of source pulse (t0) = 160 seconds
Une seule période est nécessaire pour le modèle modflow, stationnaire, mais on en met deux pour le transport pour simuler un créneau de concentration c0= 0.5 envoyé dans la colonne: sur la période 0, la concentration est c0, et elle est nulle sur la période 1.
perlen_mf = 1. perlen_mt = [160, 1320] # injection pendant 160 s laytyp = 0 # confined
Conditions aux limites pour le modèle d'écoulement:
charge constante (ibound=-1) aux deux extrémités du domaine, avec des valeurs imposées (variable strt) de façon à établir le flux de Darcy souhaité.
ibound[0, 0, 0] = -1 # constant-head at ix=1 ibound[0, 0, -1] = -1 # constant-head at ix=ncol strt[:, :, :] = 0. strt[0, 0, 0] = q*Lx
Conditions aux limites du modèle de transport:
flux massique total spécifié (troisième type) à gauche et un flux massique dispersif nul (deuxième type) à droite.
Une condition aux limites de troisième type est approximée en spécifiant un flux massique advectif (c'est-à-dire fo = qCo où q est le taux d'entrée ou de sortie à travers la frontière).
Ceci s’obtient dans le cas-test en réglant la concentration de l'afflux sur la cellule à charge constante sur la gauche à 0,05 mg/l pour la première période, et à zéro pour la deuxième période de contrainte.
c0 = 0.05
spd = {0:[0, 0, 0, c0, 1], 1:[0, 0, 0, 0., 1]}
Pour imposer une condition aux limites du deuxième type à l'aval, on place la limite droite du domaine suffisamment loin de la source pour que le panache ne l'atteigne pas dans le temps de simulation chosi.
Le type de modèle d’adsorption sélectionné, et ses paramètres, sont donnés en arguments de Mt3dRct:
sorption linéaire (Kd) isothm= 1 sp1= distribution coefficient (Kd) sp2= donné, mais non utile Freundlich : isothm= 2 sp1= Freundlich equilibrium constant (Kf) sp2= Freundlich exponent a Langmuir : isothm= 3 sp1= Langmuir equilibrium constant (Kf) sp2= total concentr' sorption sites available
On notera ici que pour la lecture des résultats il faut faire attention à l’indexation des variables de type tableau: dans le code python, les tableaux sont indexés à partir de i=0, ici pour la variable obs, alors que quand on accède à des objets produits par les codes USGS, écrits en fortran, les tableaux sont indexés à partir de i=1, comme ici pour la variable y_coord, qui désigne le même point.
Le diagramme représente, en fonction du temps, la concentration normalisée (c/c0) observée au milieu de la colonne (point (1, 1, 51), en coordonnées modflow), suivant un modèle Freundlich puis suivant un modèle Langmuir. Dans les deux cas, le schéma numérique est ADV-ULTIMATE.
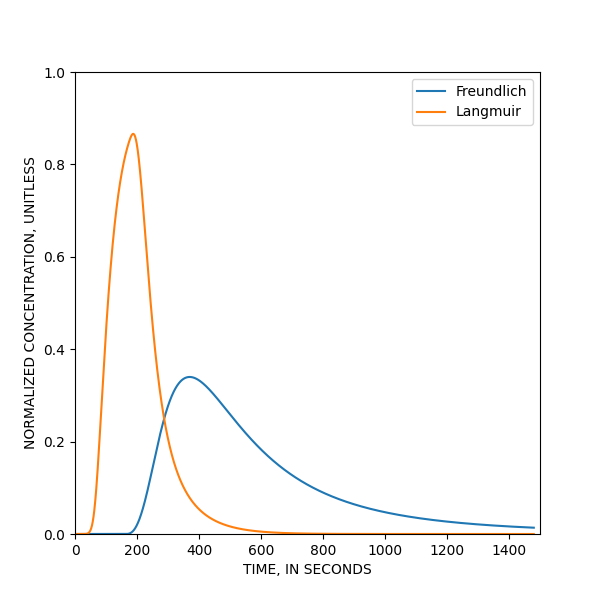
sorption linéaire == conc. adsorbée / conc. en solution = constante = Kd
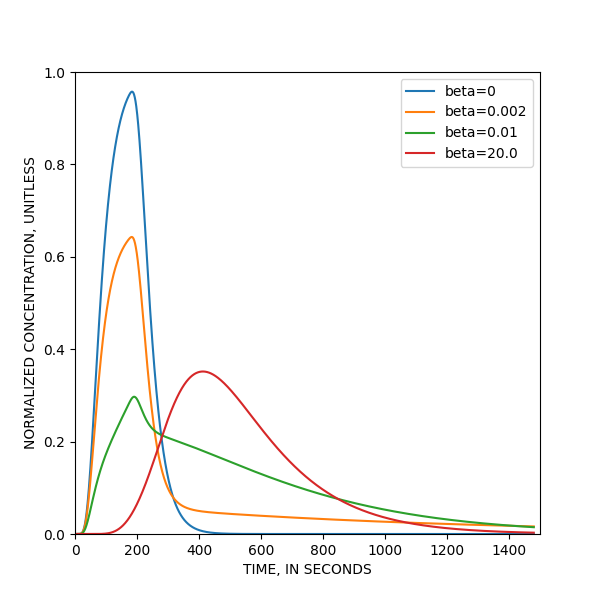
Kd= Csorbed/C, à l'équilibre C - Csorbed/Kd = C – Ceq = écart à l'équilibre si C>Ceq, alors vitesse>0, Csorbed augmente si C=Ceq, alors vitesse=0, équilibre si C<Ceq, alors vitesse<0, Csorbed diminue, désorption beta = first-order mass transfer rate between dissolved and sorbed species, 1/T Kd = distribution coefficient for the sorbed phase (linear sorption)
L'objectif de ce test (Zheng & Wang, 1999, p.138) est de valider le code sur un cas pour lequel on a une solution analytique.
C'est kle cas pour le transport 2D injecté par une source ponctuelle dans un champ d’écoulement uniforme.
paramètres du maillage
nlay = 1 nrow = 31 ncol = 46 delr = 10 # mètres delc = 10 # mètres delv = 10 # mètres
paramètres nappe
v = 1./3. # mètre/jour prsity = 0.3 q = v * prsity
paramètres transport
al = 10. # dispersivité alpha trpt = .3 # longitudinal/horizontal transverse dispersivity q0 = 1. # débit de fluide injecté en [0,15,15] c0 = 1000. # concentration injectée
l’injection s’implémente dan s le code en deux endroits:
spd= [[0, 15, 15, q0]] wel = flopy.modflow.ModflowWel(mf, stress_period_data=spd)
spd = {0:[0, 15, 15, c0, 2]}
ssm = flopy.mt3d.Mt3dSsm(mt, stress_period_data=spd)
Cartes du panache à la fin de la période de simulation (365 jours) >>
Diagrammes de Zheng & Wang, fig. 35, qui donnent aussi les solutions analytiques du cas étudié. >>

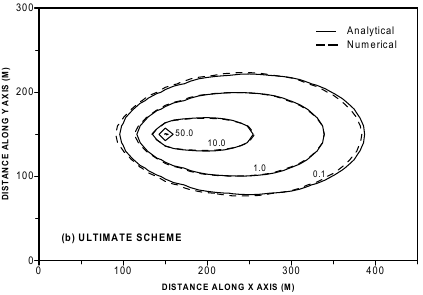
Zheng & Wang, 1999, p.140
Domaine à une couche, de 31 par 31 cellules, en aquifère confiné.
Les cellules des quatre bords du domaine ont des charges piézo fixées à zéro.
ibound = np.ones((nlay, nrow, ncol), dtype=np.int) * -1 ibound[:, 1:nrow - 1, 1:ncol-1] = 1 # x,y coords inside the domain strt = 0. # heads along borders held constant at 0
le programme compare les performances de différents solveurs:
mixelm= -1 : solveur ULTIMATE mixelm= -0 : solveur Upstream FD, avec TTSMULT=1.0 mixelm= -0 : solveur Upstream FD, avec TTSMULT=1.5 TTSMULT= nombre de pas de temps de calcul de transport pour un pas de temps en MODFLOW.
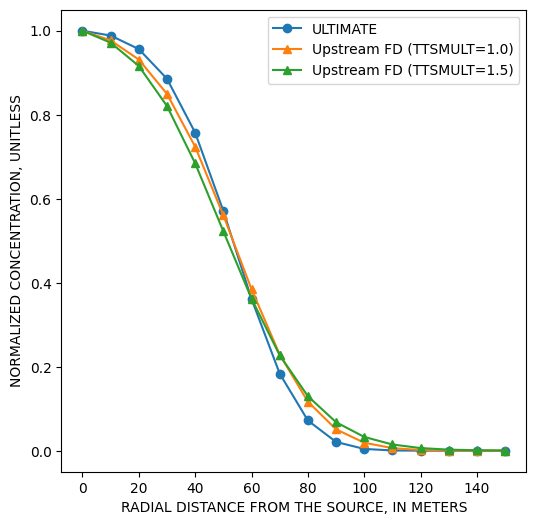
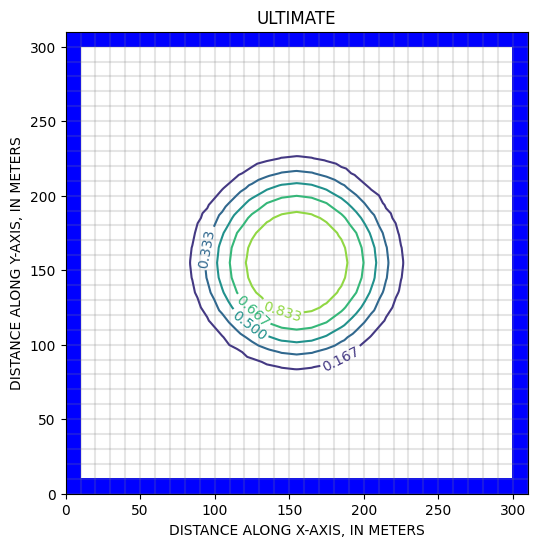
Zheng & Wang, 1999, p.144
On simule ici l’évolution de la concentration à un puits injecteur-extracteur dans un aquifère confiné.
De l’eau, avec une concentration donnée C0 d’une espèce, est injectée dans un puits, pendant un temps donné (2.5 ans). A la fin de cette période, la pompe est inversée et le contaminant est repompé hors de l’aquifère, pendant 7.5 ans.
paramètres de l’écoulement :
hk = 0.005 * 86400 # 0.005 ft/sec laytyp = 0 # confined nper_mf= 2 perlen_mf = [912.5, 2737.5] # 2.5 years, 7.5 years
périodes d’injection et de pompage :
welspd = {0: [[0, 15, 15, q0]], # inject
1: [[0, 15, 15, -q0]]} # pump
paramètres du transport :
prsity = 0.30 al = 100. trpt = 1. c0 = 100. nper_mt= nper_mf perlen_mt = perlen_mf
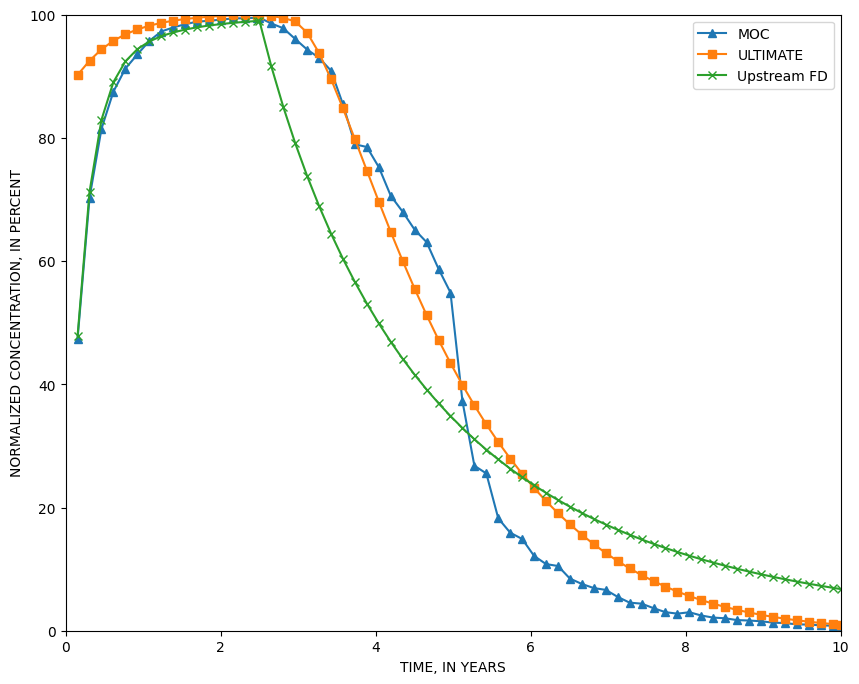
Zheng & Wang, 1999, p.145
Hydraulic conductivity of the aquifer = 0.5 m/day Porosity = 0.2 Longitudinal dispersivity = 10 m Ratio of horizontal transverse to longitudinal dispersivity = 0.3 Ratio of vertical transverse to longitudinal dispersivity = 0.3 Volumetric rates of injection = 0.5 m3/day Relative concentration of the injected water = 100 percent Simulation time = 100 days
le nombre de Péclet est assez bas: 10/10= 1
( Péclet= v . deltaX / Dxx = v.deltaX / (alpha.v) = deltaX / alpha )
les différents schémas numériques devraient donc convenir.
Conditions aux limites pour l’écoulement :
ibound = np.ones((nlay, nrow, ncol), dtype=np.int) ibound[:, :, 0] = -1 # constant imposed head on left side = h1 ibound[:, :, -1] = -1 # constant imposed head on right side = 0 strt = np.zeros((nlay, nrow, ncol), dtype=np.float) h1 = q * Lx strt[:, :, 0] = h1 # imposed head on left side
Autrement dit, ibound=0 partout, sauf sur la colonne de gauche (iy=0) et celle de droite (iy=-1), où ibound=-1, ce qui signifie que head est constant, imposé à la valeur initiale strt=q*Lx à gauche et 0 à droite, de façon à avoir un flux constant dans le domaine.
Conditions d’injection :
L’injecteur est situé en [6,7,2] en python, c’est à dire à la couche ilay=6, correspondant à 7 en MODFLOW, la plus profonde (en MODFLOW, le z du maillage pointe vers le bas), et aux coordonnées MODFLOW x, y= 8,3.
Il y a une seule période, de 100 jours.
- en flow, spd=[[6, 7, 2, q0]], injection d’un flux q0 constant
- en transport : spd = {0:[6, 7, 2, c0, 2]}, ce flux porte une concentration de100.
Les cartes des concentrations montrent le transport horizontal vers la droite par advection associé à un étalement latéral et vers le haut par la diffusion.
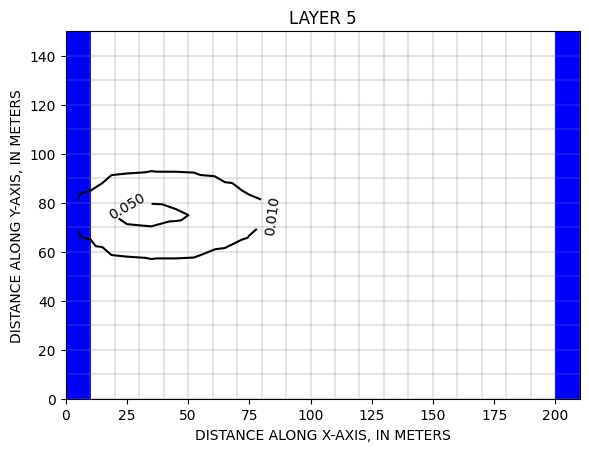
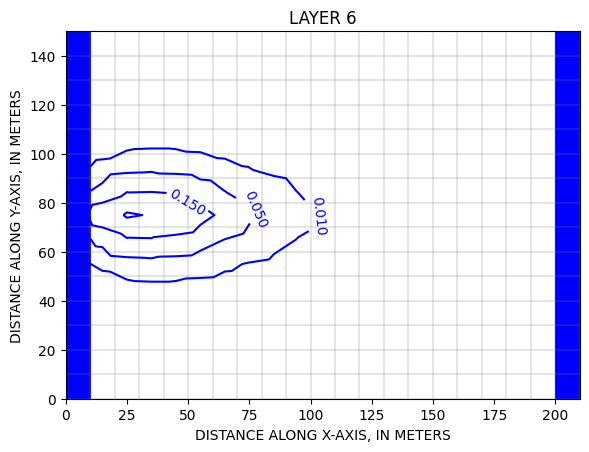
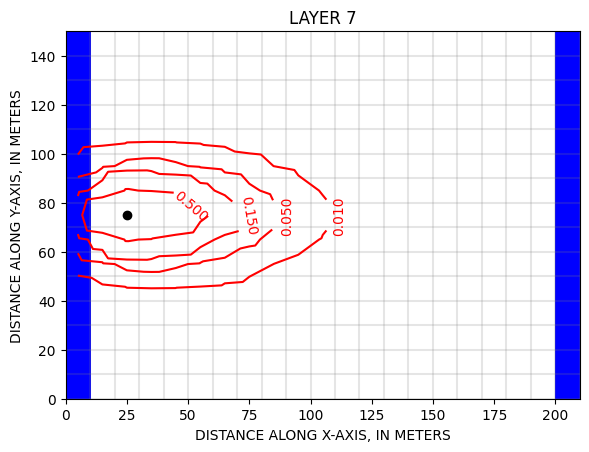
Zheng & Wang, 1999, p.146
Le domaine a une longueur de 250 m et une profondeur allant de 6,5 m le long de la frontière gauche et 5,37 m le long de la frontière droite.
L'écoulement est stationnaire.
conditions aux limites pour l’écoulement >>:
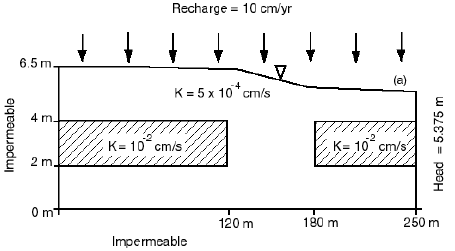
Les limites à gauche et inférieure sont imperméables, la charge hydraulique est uniforme et constante, à 5.375 m le long de la frontière droite.
propriétés hydrauliques :
La nappe phréatique le long de la limite supérieure du système reçoit une recharge uniforme de 10 cm / an.
L'aquifère est constitué d'un sable limoneux à grain fin (KH = 5.10-4 cm/sec) à l'intérieur duquel se trouvent deux lentilles de sable à grain moyen à conductivité plus élevée (KH = 10E-2 cm / sec).
La conductivité hydraulique est supposée isotrope.
conditions aux limites pour le transport >> :
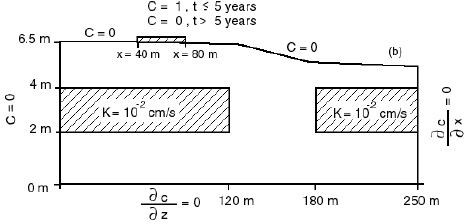
Initialement, le contaminant est présent sur la première couche, de x= 40 m à x= 80 m, à une concentration relative de 1. La concentration est nulle partout ailleurs.
La source est active pendant 5 ans, puis elle est supprimée, et la concentration le long du haut du domaine revient à une valeur uniforme de zéro.
propriétés du milieu :
Une porosité uniforme de 0,35 est attribuée au domaine, la dispersivité longitudinale (DL) et transversale verticale (DTV) est de 0,5 m et 0,005 m, respectivement, et le coefficient de diffusion effectif est de 1,34.E-5 cm2 / sec.
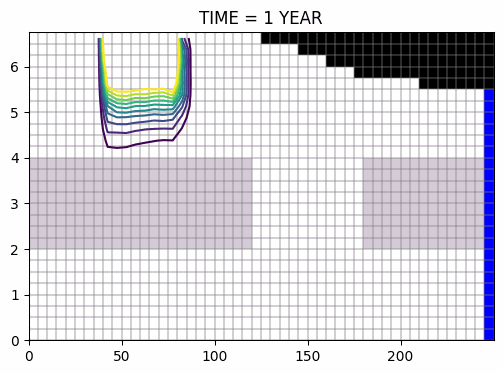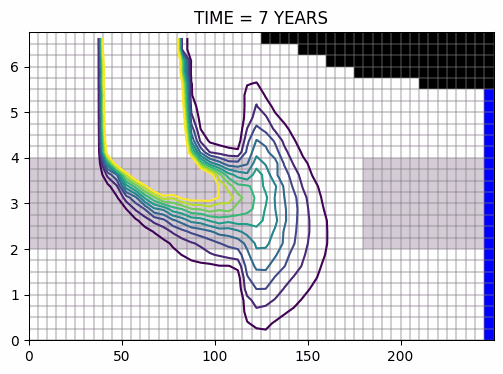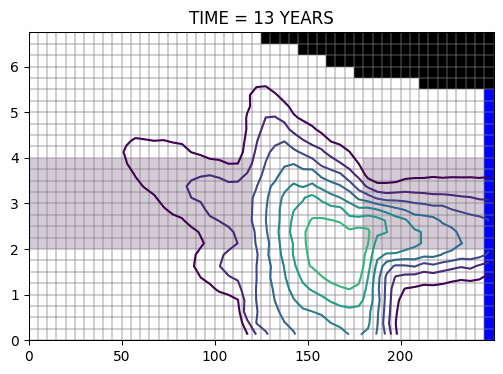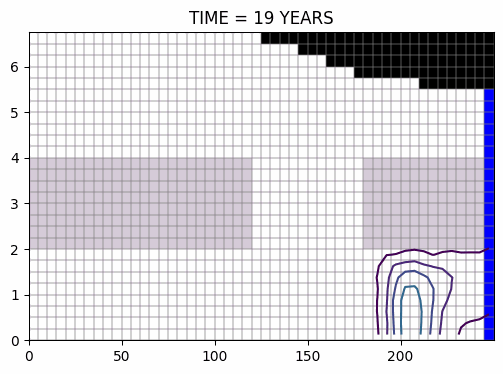
évolution du panache, pendant puis après la pollution >>
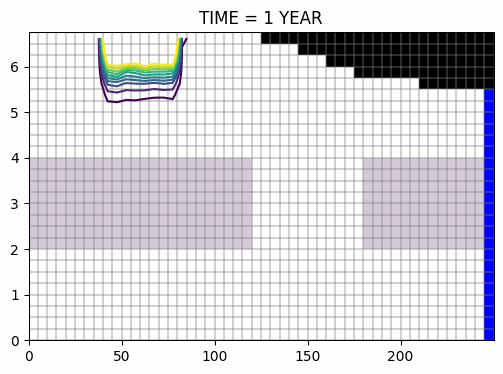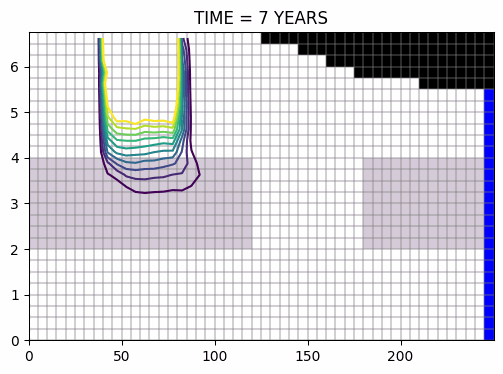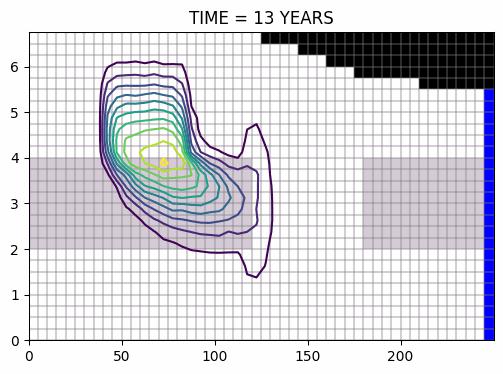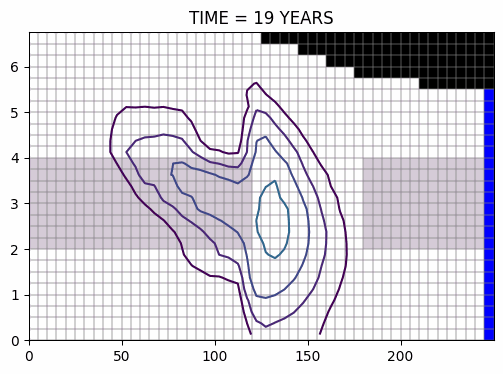
mêmes conditions, excepté pour la recharge, 3 fois plus élevée >>
conditions aux limites pour l’écoulement:
A l'est et à l'ouest, limites sans écoulement.
Au nord, frontière à charge constante et uniforme de 250 m.
Au sud, frontière à charge fixe, variant linéairement de 20 m à l'Ouest à 52,5 m à l'Est.
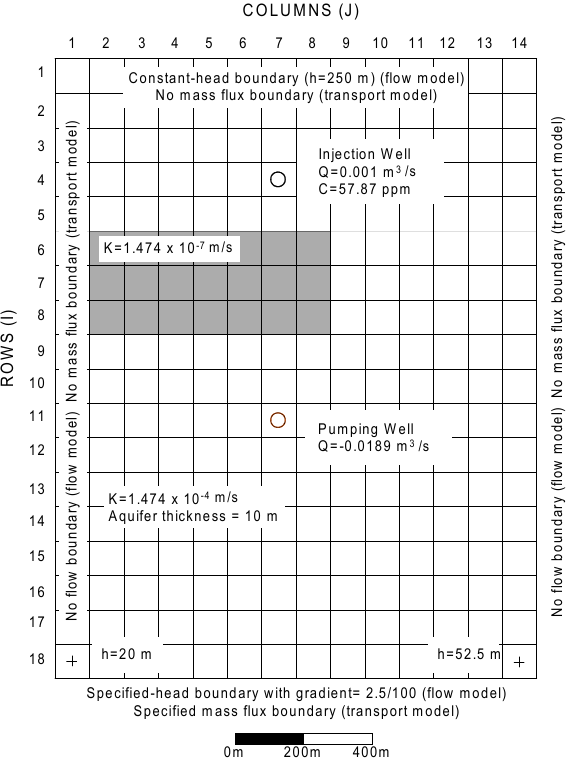
propriétés du milieu :
L'eau d'une concentration donnée en soluté est injectée dans l'aquifère à travers un puits entièrement pénétrant, tandis qu'un puits de pompage situé en aval élimine la masse de soluté de l'aquifère.
Entre le puits d'injection et le puits de pompage il y a une zone moins perméable, dans laquelle la conductivité hydraulique est 1000 fois inférieure à celle ailleurs dans le domaine.
conditions aux limites du modèle de transport :
Bordures est, ouest et nord: frontières sans flux de masse.
Bordure sud: frontière à flux de masse advectif, agissant comme une ligne de puits ponctuels retirant de la masse de l'aquifère. La masse prélevée est égale au flux entrant par les cellules à charge constante multiplié par la concentration dans les cellules.
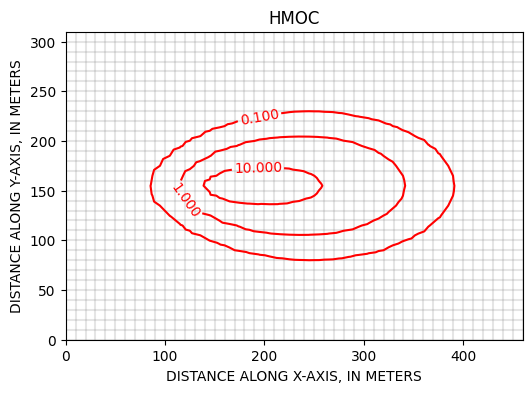
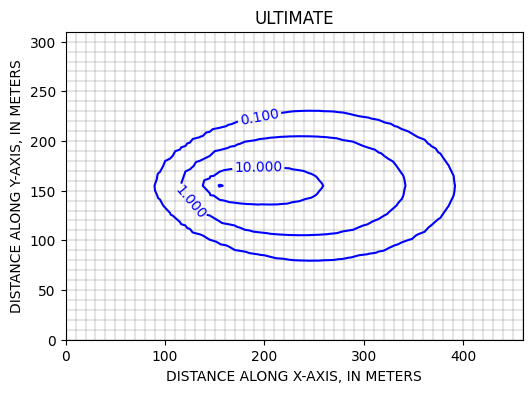
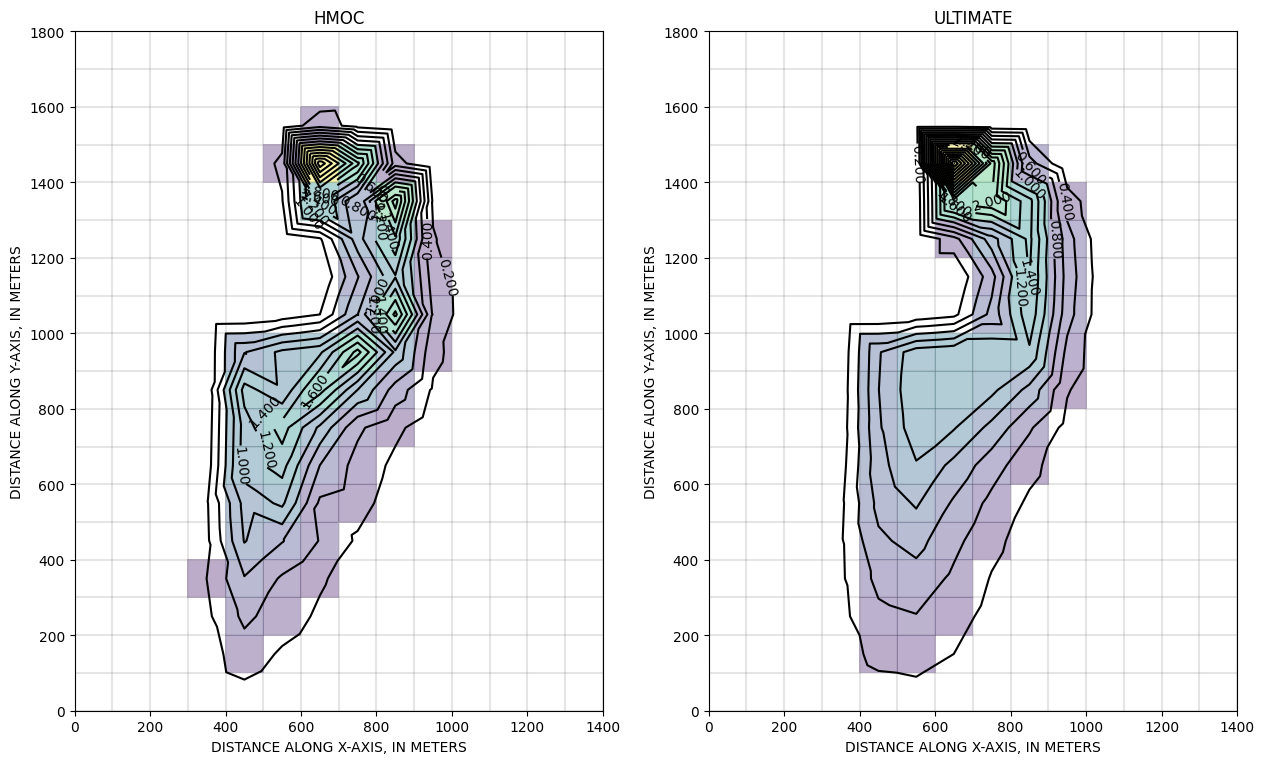
Cartes du panache après une année, calculées suivant les schémas HMOC et ULTIMATE >>
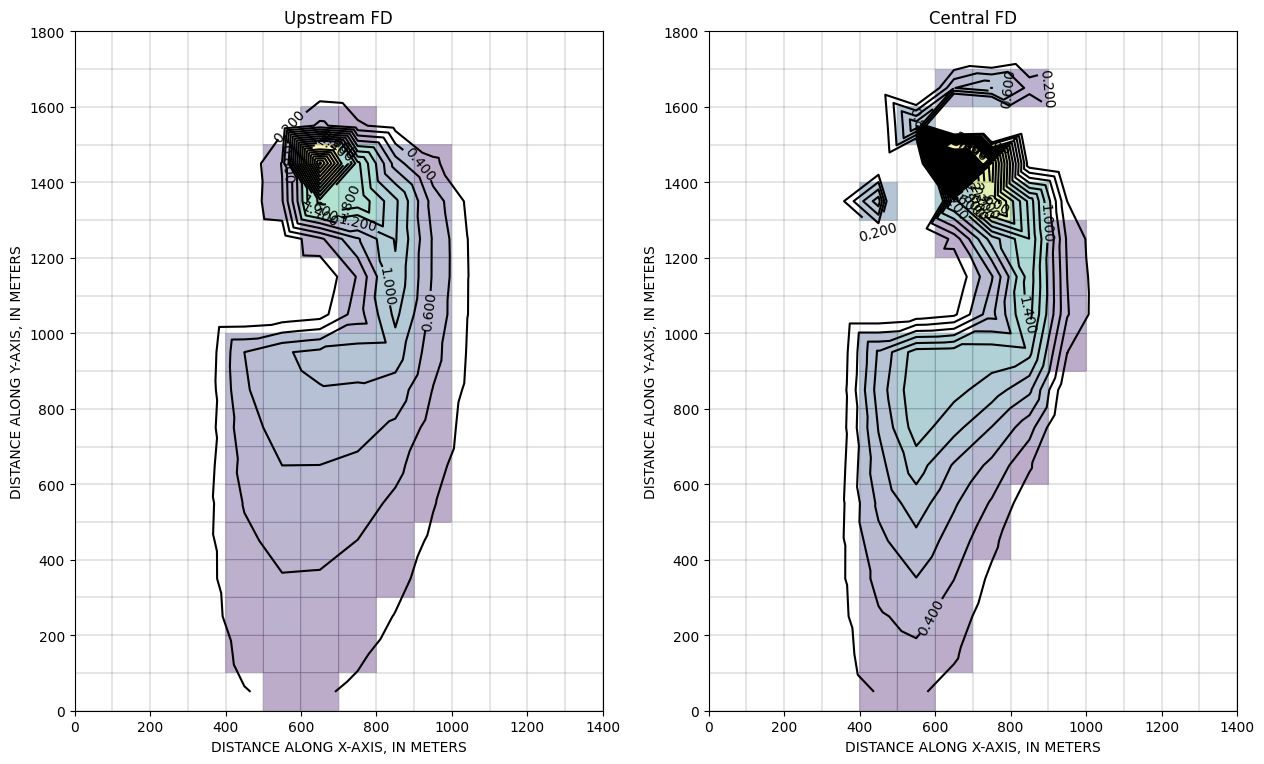
Cartes du panache après une année, calculées suivant les schémas Upstream-FD et Central-FD >>
Evolution du panache au cours du temps, calculée suivant le schémas ULTIMATE >>
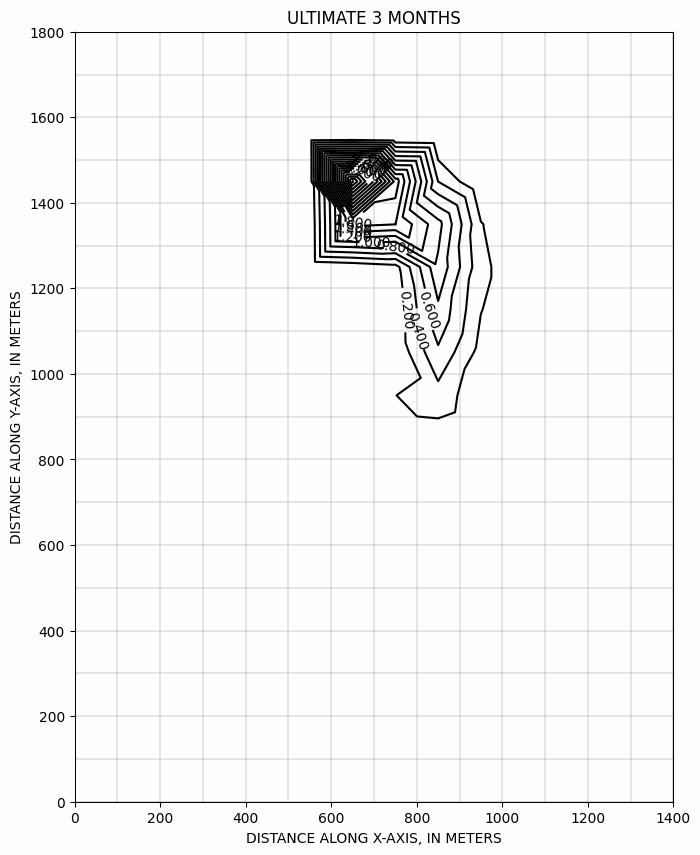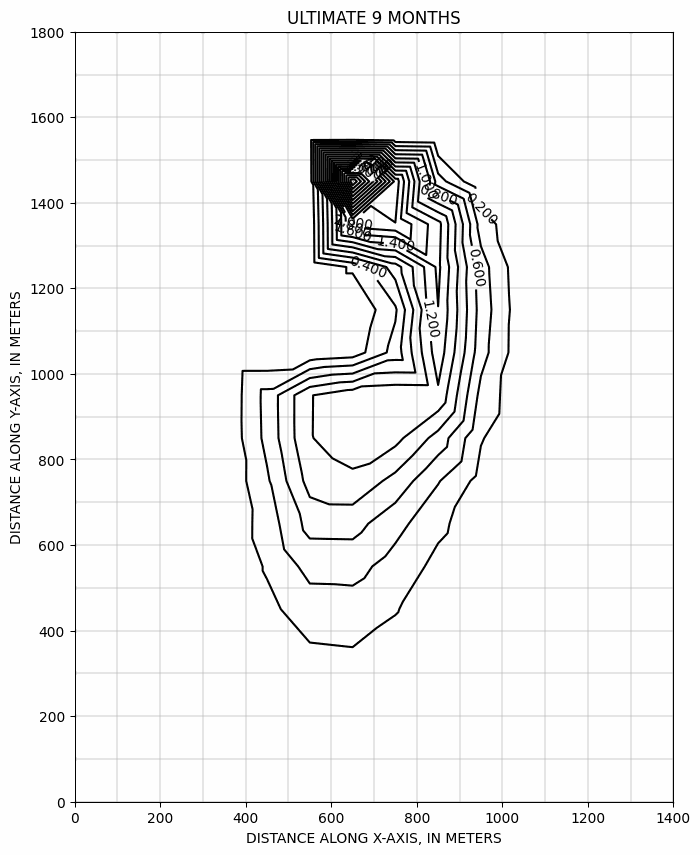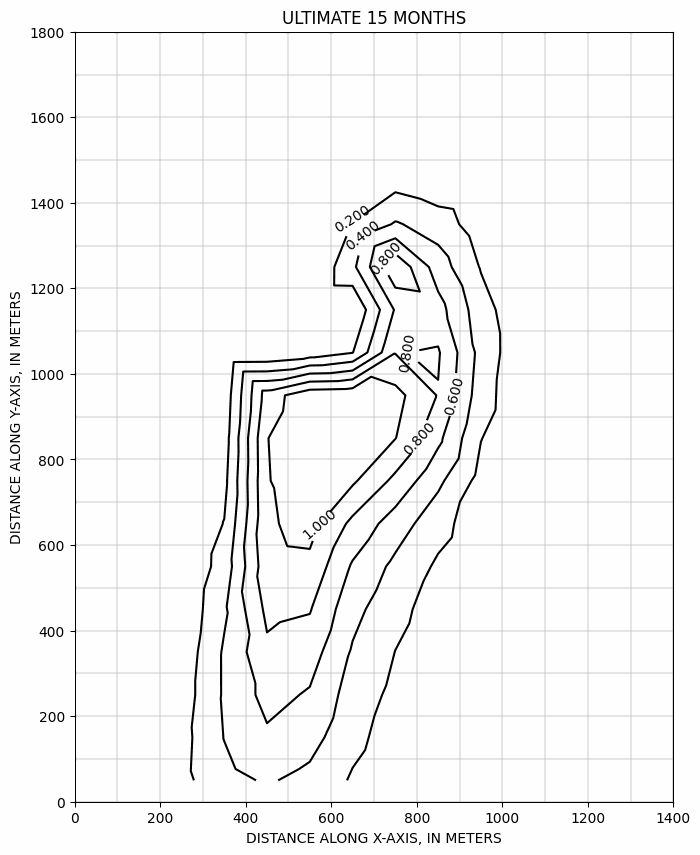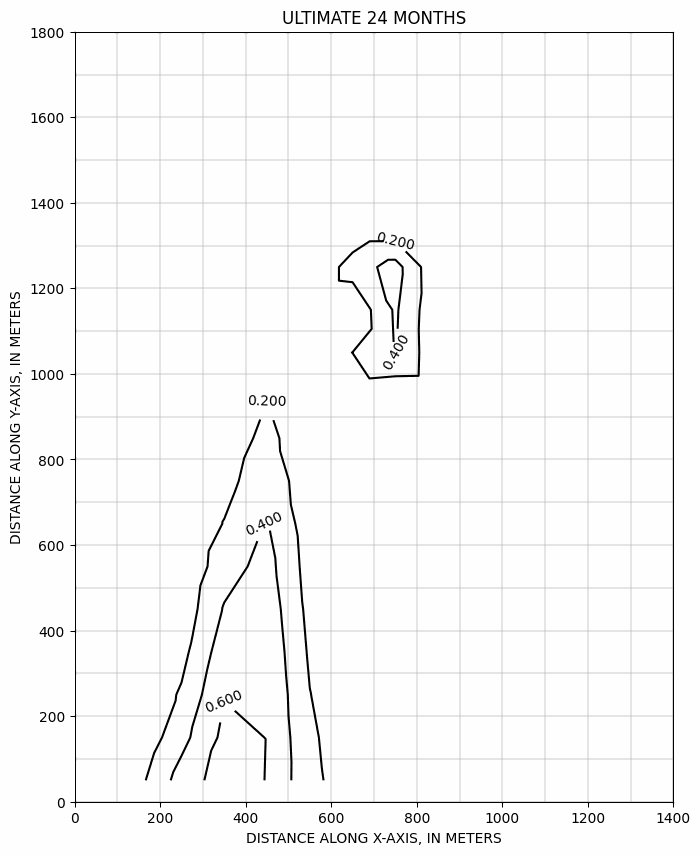
Evolution du panache avec un pompage 10x, calculée suivant le schémas ULTIMATE >>
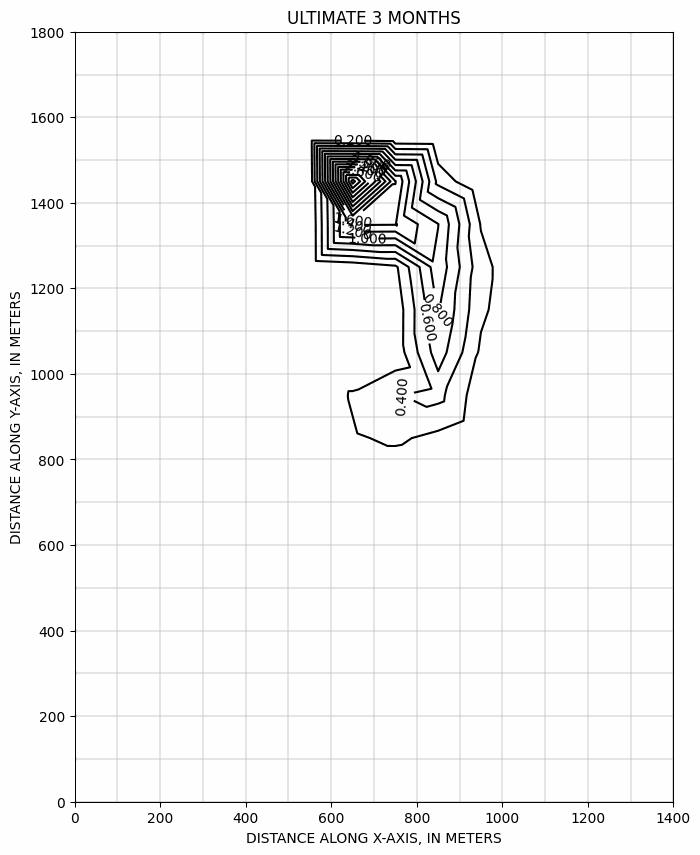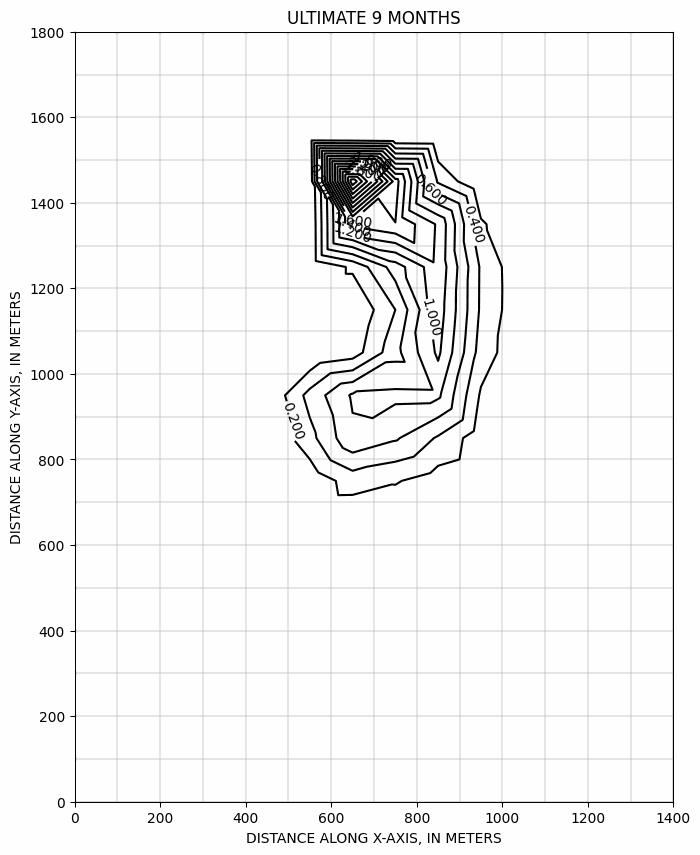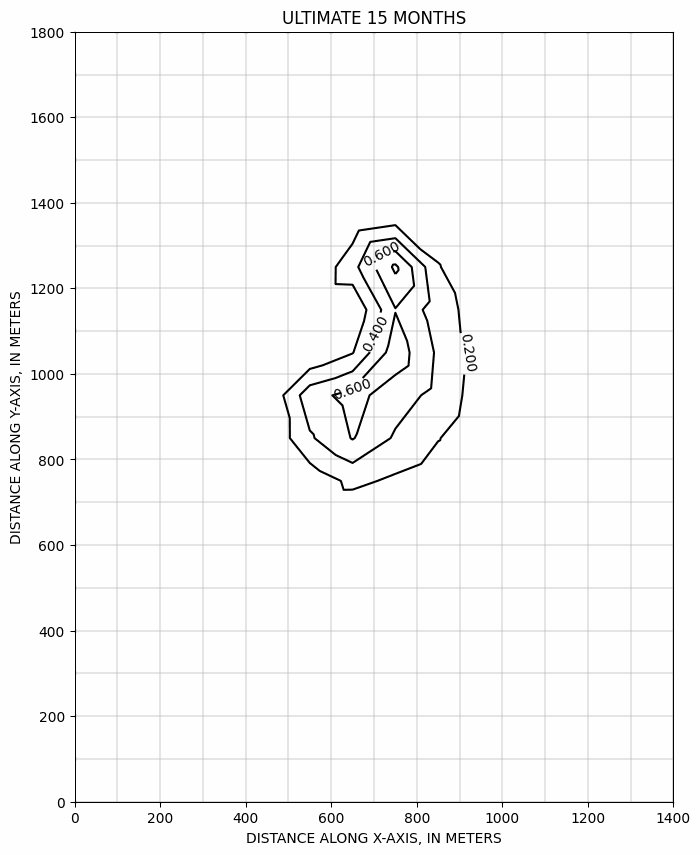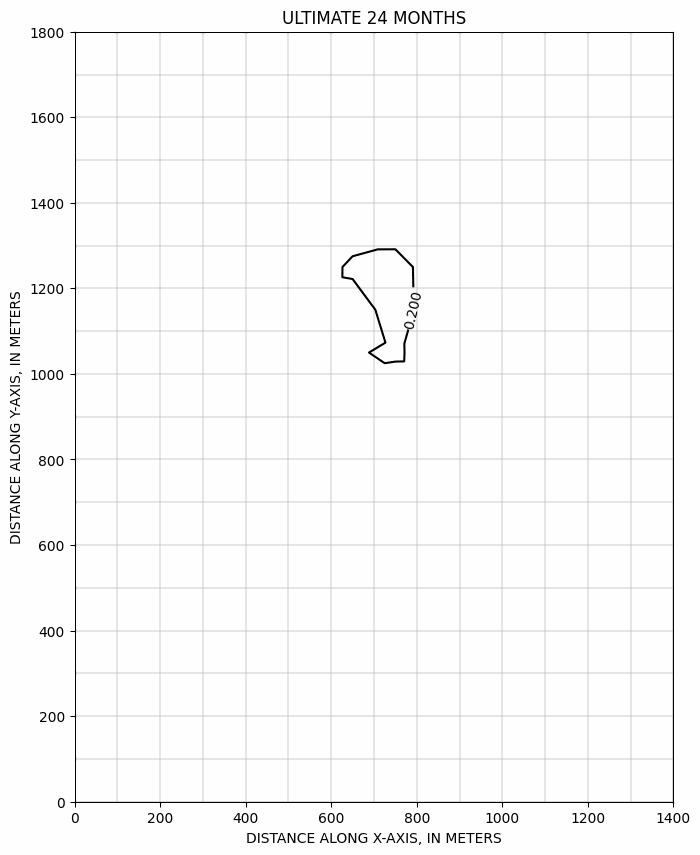
évolution de la concentration au puits de pompage, dans les différents schémas numériques, et avec un maillage deux fois plus serré >>