
01_tutorial_1.py: montage avec flopy d'un modèle MODFLOW simple, pour un aquifère confiné, en état stationnaire
le modèle va faire appel aux "packages" MODFLOW suivants:
A chaque package correspondra un fichier d'entrée, qui sera créé par flopy avec les paramètres passés en arguments des fonctions flopy correspondantes.
On a souligné ici les appels aux fonctions flopy.
On commence par importer les librairies nécessaires. Il peut s’agir de librairies intégrées à python, comme os, sys, platform, ou de librairies qui ont nécessité une installation spécifique, comme numpy et flopy. Comme on le voit ici dans le cas de numpy, il est possible de renommer localement une librairie, simplement pour simplifier le code : alors, au lieu d’écrire numpy.array pour gérer un objet de type array implémenté par numpy, on écrira plus simplement np.array.
import os import sys import platform import numpy as np import flopy
On s'intéresse ici à une simulation d'écoulement dans un aquifère, on va donc uiliser MODFLOW (Flopy peut gérer aussi d'autres programmes de la suite USGS), et en l'occurrence la version 2005, qui est la plus récente du modflow classique.
On doit informer le chemin, exe_name, de l'exécutable USGS.
(dans notre cas, le répertoire USGS a été au préalable ajouté au PATH du système, c'est donc simplement le nom du programme).
workdir désigne le répertoire où seront écrits les fichiers MODFLOW du modèle.
exe_name = 'mf2005'
if platform.system() == 'Windows': exe_name = 'mf2005.exe'
workdir = os.path.join('.', 'data')
Pour créer un modèle, il nous faut en outre un nom, modelname, et un espace de travai, model_ws, répertoire où seront écrits les fichiers MODFLOW qu'appellera modflow.exe au moment de l'exécution. La procédure join, dans le module os.path, sert simplement à assurer une écriture correcte des séparateurs de répertoires, qu'on soit en linux (slash) ou en windows (backslash).
modelname = 'tutorial1' model_ws = os.path.join(workdir, modelname)
On dispose maintenant des données (nom du modèle, chemin de l'exécutable, espace de travail) nécessaires à la création d'un modèle Modflow du module modflow de la librairie flopy.
mf = flopy.modflow.Modflow(
modelname= modelname,
model_ws= model_ws,
exe_name= exe_name)
Dans le code modelname= modelname, on a deux fois le même nom modelname, pour désigner deux choses différentes, à gauche un mot réservé de la liste des paramètres possibles pour un objet Modflow de la librairie flopy.modflow, et à droite le nom d’une variable de notre script, qui contient la valeur 'tutorial1'.
On dispose maintenant d'un modèle Modflow, appelé mf, que l'on va pouvoir 'renseigner'.
Le domaine considéré est une couche horizontale de 1000 mètres sur 1000 et de 50 mètres d'épaisseur.
Lx = 1000. Ly = 1000. ztop = 0. zbot = -50.
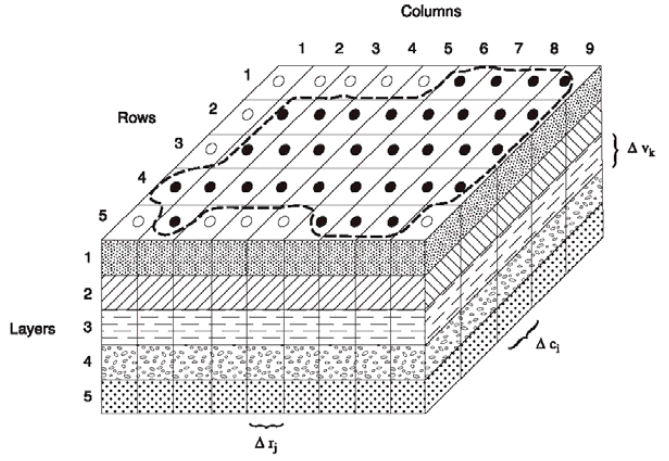
Ce domaine monocouche est discrétisé suivant un maillage orthogonal de 20 colonnes suivant x par 20 lignes suivant y.

|

|
Les noms des paramètres (delr, delc, delv) de ModflowDis se réfèrent à la nomenclature usuelle de modflow.
nlay, nrow, ncol = 1, 20, 20 delv = (ztop -zbot) / nlay delr = Lx/ncol delc = Ly/nrow botm = np.linspace(ztop, zbot, nlay + 1)
Ces paramètres de maillage sont renseignés dans le modèle mf par l'appel à la fonction ModflowDis de flopy.modflow
dis = flopy.modflow.ModflowDis(
mf,
nlay, nrow, ncol,
delr=delr, delc=delc,
top=ztop, botm=botm[1:])
Le tableau ibound, de dimensions (nlay, nrow, ncol), renseigne le statut de chaque cellule
Dans notre modèle, toutes les cellules sont actives, et la charge est contrainte sur les limites Ouest (colonne 0) et Est (colonne -1) du domaine. En python, l'indexation des tableaux débute à 0, et l'indice -1 désigne par convention le dernier élément d'un tableau. On note aussi ici l'utilisation du ':' pour adresser l'ensemble des valeurs d'une couche, ligne ou colonne.
ibound = np.ones((nlay, nrow, ncol), dtype=np.int32) ibound[:, :, 0] = -1 # icol= 0 means first column, for all x and z ibound[:, :, -1] = -1 # icol= -1 means last column, for all x and z if modif1: ibound[:,4:8,4:8]= 0
On doit également renseigner, pour les cellules à charge donnée, les valeurs de ces charges. Cela se fait par le tableau strt, de dimensions (nlay, nrow, ncol), des valeurs des charges au départ. On a ici une charge initiale (et constante en système stationnaire) à 10 mètres sur la frontière Ouest (première colonne) et à 0 sur la frontière Est.
strt = np.ones((nlay, nrow, ncol), dtype=np.float32) strt[:, :, 0] = 10. # starting head value on first column strt[:, :, -1] = 0. # starting head value on last column
Ces paramètres étant initialisés, on peut mettre à jour le modèle en appelant la fonction ModflowBas comme suit:
bas = flopy.modflow.ModflowBas(
model= mf,
ibound=ibound,
strt=strt)
Le package LPF concerne les propriétés hydrodynamiques des couches, en particulier les conductivités hydrauliques: le tableau hk, de dimensions (nlay, nrow, ncol), correspond aux conductivités suivant l'axe x (et suivant y puisqu'ici aucune anisotropie n'est introduite); le tableau vka (vertical) correspond aux conductivités suivant z (vka est ici un scalaire qui sera la valeur homogène du tableau vka).
hk= 10. if modif==2: hk= np.ones((nlay, nrow, ncol), dtype=np.float32) *10. hk[:, 4:8, 4:8 ]= 500. hk[:,13:17,13:17]= 0.1
Le modèle est alors mis à jour. Le paramètre laytyp n'étant pas listé en entrée, il sera à sa valeur par défaut, laytyp=0, qui impose un modèle confiné (nappe captive).
lpf = flopy.modflow.ModflowLpf(
mf,
hk= hk, # horizontal hydraulic conductivity
vka=10., # vertical hydraulic conductivity
ipakcb=53) # cell-by-cell budget data will be saved
Ce module fait appel à la notion de "stress periods" de modflow: ce sont les intervalles de temps pendant lesquels les contraintes du modèle (les données d'entrée du modèle, par exemple le débit de pompage d'un puits, et autres conditions limites) sont constantes. Dans flopy, la définition des "stress periods" utilise les objets pythoniens de "tuple" et de "dictionary". Un tuple est une collection d'objets (listée entre parenthèses), qui différe de la list (listée entre crochets) par le fait qu'elle ne peut être modifiée, la liste étant dynamique. Les tuples sont utilisés dans les dictionary, qui permettent de stocker des données sous une forme "key:value". Dans le cas présent, le modèle est stationnaire, les contraintes sont donc invariables, et il n'y a qu'une "stress period", d'indice 0, et un seul pas de temps, valant 0; aussi le dictionnaire ne contient qu'un élément, avec pour clé le tuple (0,0) et pour valeur une liste d'instructions d'écriture modflow.
spd = {(0, 0): ['print head', 'print budget', 'save head', 'save budget']}
oc = flopy.modflow.ModflowOc(
model= mf,
stress_period_data=spd,
compact=True)
pcg = flopy.modflow.ModflowPcg(mf)
Les différents paramètres du modèle ayant été renseignés, la méthode write_input du modèle est utilisée pour écrire les fichiers d'entrée modflow, et la méthode run_model pour lancer l'exécution de mf2005.
mf.write_input() success, buff = mf.run_model()
On a donc utilisé flopy en pre-processeur de modflow, mais flopy fournit également des outils pour le post-processing: pour lire les fichiers de sortie ( module flopy.utils.binaryfile), dont certains sont sous forme binaire (suffixe .hds), et pour visualiser les résultats ( module flopy.plot), en association avec la libraitie matplotlib.
import matplotlib.pyplot as plt import flopy.utils.binaryfile as bf fig = plt.figure(figsize=(8,8)) plt.subplot(1, 1, 1, aspect='equal') hds = bf.HeadFile(os.path.join(model_ws,modelname) + '.hds') head = hds.get_data(totim=1.0) levels = np.arange(1, 10, 1) extent = (delr / 2., Lx - delr / 2., Ly - delc / 2., delc / 2.) plt.contour(head[0, :, :], levels=levels, extent=extent) jplot+=1 plt.savefig(figname+str(jplot)+".png")
On utilise ici le module flopy.utils.binaryfile pour lire le fichier des charges, et la fonction contour de matplotlib pour visualiser le champ des charges dans la première (ici uinique) couche du modèle, couche 0 du tableau head[:, :, :].

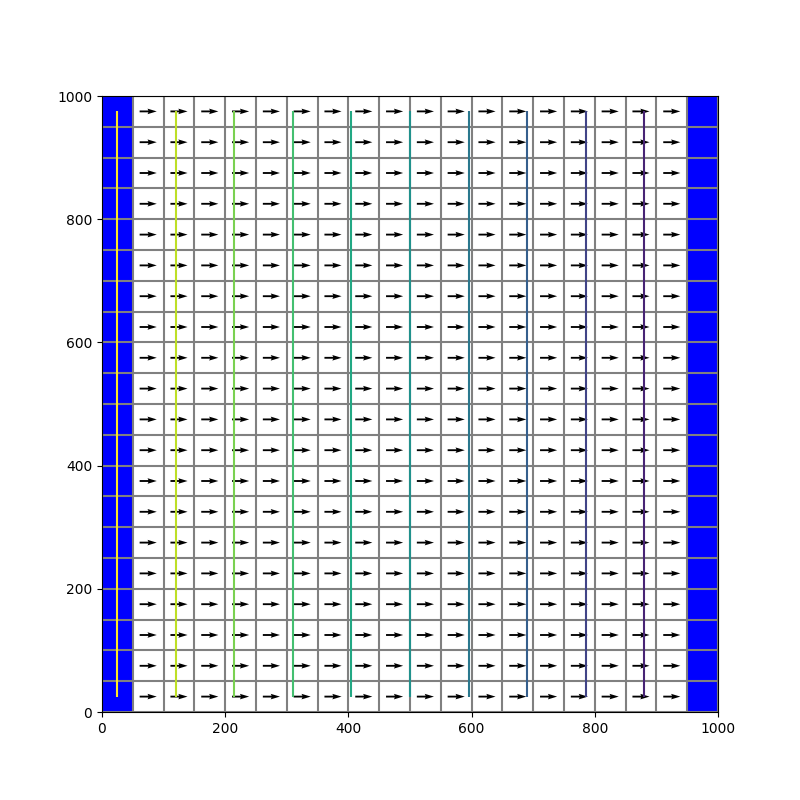
Des fonctions de visualisation sont aussi fournies par flopy, par exemple ici l'objet PlotMapView du module flopy.plot, qui inclut les méthodes plot_ibound (représente le tableau ibound, donc le statut des cellules), plot_grid, contour_array (équivaut à plt.contour), plot_discharge (champ de vecteurs) illustrées ici.
fig = plt.figure(figsize=(8,8)) ax = fig.add_subplot(1, 1, 1, aspect='equal') hds = bf.HeadFile(os.path.join(model_ws,modelname)+'.hds') times = hds.get_times() print(times) head = hds.get_data(totim=times[-1]) levels = np.linspace(0, 10, 11) cbb = bf.CellBudgetFile(os.path.join(model_ws,modelname)+'.cbc') kstpkper_list = cbb.get_kstpkper() frf = cbb.get_data(text='FLOW RIGHT FACE', totim=times[-1])[0] fff = cbb.get_data(text='FLOW FRONT FACE', totim=times[-1])[0] mapview = flopy.plot.PlotMapView(model=mf, layer=0) qm = mapview.plot_ibound() lc = mapview.plot_grid() cs = mapview.contour_array(head, levels=levels) quiver = mapview.plot_discharge(frf, fff, head=head) jplot+=1 plt.savefig(figname+str(jplot)+".png")